Metoda elementów skończonychmilenin/Dydaktyka/MES/MES2005a.pdf · Metoda Elementów Skończonych...

Metoda Elementów SkończonychMilenin Andrzej

Metoda elementów skończonych

Wykłady: prof. dr hab. inŜ. Andrzej Milenin

Pok. B5 710

E-mail: [email protected]


Literatura

• M. Pietrzyk Metody numeryczne w przeróbce plastycznej metali // AGH, Kraków, 1992

• O.C.Zienkiewicz, R.L.Taylor The Finite Element Method// Butterworth Heinemann, 3 vol, 5-th Edition, London, 2000

• Zienkiewicz O.C., Metoda elementów skończonych, Arkady, Warszawa, 1972.


1. Główna koncepcja metody elementów skończonych

2. Dyskretyzacja ośrodka, typy elementów skończonych

3. Podstawy rachunku wariacyjnego

4. Rozwiązanie stacjonarnych i niestacjonarnych zadań, w których niewiadomą jest funkcja skalarna

5. Rozwiązanie zadań, w których niewiadomą jest funkcja wektorowa

6. Opracowanie programu do symulacji procesów przeróbki plastycznej za pomocą MES

SPIS TREŚCI


- Metoda elementów skończonych (MES) jest metodęrozwiązywania równań róŜniczkowych, spotykanych w fizyce i technice.

- Powstanie tej metody jest związane z rozwiązywaniem zagadnieńbadań kosmicznych (1950 r.).

- W obecnej chwili MES jest wykorzystywana praktycznie we wszystkich dziedzinach nauki (transport masy, transport ciepła, przepływ cieczy, pola napręŜeń).

Po raz pierwszy metoda ta była opublikowana w pracy :Turner M.J., Clough R.W., Martin H.C., Topp L.J. Stiffness and Deflection Analysis of Complex Structures // J.Aeronavt. Sci., 1956, #23, p. 805-824.

Wstęp


Przykład z technologii kucia matrycowego


Przykład z technologii walcowania


Główna idea MES polega na tym, Ŝe dowolną ciągłą wartość (np. temperaturę) moŜna zamienić na model dyskretny.

Model ten jest oparty na ograniczonej ilości węzłów, które tworząograniczoną ilość elementów skończonych

1. Główna koncepcja metody elementów skończonych


1. W rozpatrywanym ośrodku bierzemy pod uwagę ograniczoną ilość punktów(węzłów).

2. Wartości temperatury (lub innej funkcji) w kaŜdym węźle definiujemy jako parametr, który musimy wyznaczyć.

3. Strefa wyznaczenia temperatury dzieli się na ograniczoną ilość pod-stref, które nazywamy elementami skończonymi.

4. Temperaturę aproksymuje się na kaŜdym elemencie za pomocą wielomianu, który wyznaczony jest za pomocą węzłowych wartości temperatury. Wyznacza się go w taki sposób, aby zachować warunek ciągłości temperatury na granicach elementów.

5. Węzłowe wartości temperatury muszą być dobrane w taki sposób, aby zapewnićnajlepsze do rzeczywistego przybliŜenie pola temperatury. Taki dobór wykonywany jest za pomocą minimalizacji funkcjonału, który odpowiada róŜniczkowemu równaniu przewodzenia ciepła.

1.1. Algorytm MES


1.2 WaŜniejsze zalety MES w porównaniu do innych metod

1. Własności materiału elementów niekoniecznie muszą być jednakowe. To daje moŜliwość wykorzystania MES do materiałów wielofazowych, jak równieŜ do materiałów, których własności są funkcją temperatury.

2. Ośrodek o skomplikowanym kształcie moŜe być zaproksymowana z duŜądokładnością za pomocą elementów krzywoliniowych.

3. Wymiary elementów mogą być objętościowo róŜne. To daje moŜliwośćpowiększania lub zmniejszania wymiarów elementów w pewnych strefach rozpatrywanej objętości.

4. Za pomocą MES moŜna uwzględniać nieliniowe warunki brzegowe.


1.3. Typy rozpatrywanych zadań

Rozwiązanie zadań, w których niewiadomą jest funkcja skalarna

1. Przypływ ciepła w stanie ustalonym 2. Niestacjonarny przepływ ciepła 3. Dyfuzji składnika w ciałach stałych4. Dyfuzja w czasie krzepnięcia materiałów dwufazowych5. Przypływ ciepła w czasie krzepnięcia materiałów

Rozwiązanie zadań, w których niewiadomą jest funkcja wektorowa

1. Stan napręŜeń spręŜystych w ciałach o skomplikowanym kształcie obciąŜonych siłami2. NapręŜenia cieplne w ciałach o skomplikowanym kształcie3. Zadania teorii płynów 4. Zadania teorii plastyczności


2. Dyskretyzacja ośrodka

Rozkład temperatury w jednowymiarowym pręcie

Główna koncepcja MES moŜe być pokazana na jednowymiarowym przykładzie aproksymacji ciągłego pola temperatury w pręcie


Rozpatrzmy ciągły rozkład temperatury t(x) na odcinku 0L wzdłuŜosi X analizując pięćwęzłowych punktów na odcinku 0L

2.1 Dyskretyzacja ośrodka jednowymiarowego

Punkty węzłowe (a) i ewentualni wartości t(x) (b).


•Rozdzielenie ośrodka 0L na elementy moŜna wykonać na róŜne sposoby.

•Na przykład moŜna wykorzystaćdwa sąsiednie węzły.

•Wtedy otrzymamy cztery elementy, lub rozdzielić strefę na dwa elementy, z których kaŜdy zawiera trzy węzły.

Rozdzielenie ośrodka na elementy

Podział ośrodka na elementy pierwszego (a) i drugiego (b) stopnia.


Wielomian aproksymujący wyznaczamy na podstawie wartości temperatury w węzłach elementu. W przypadku rozdzielenia rozpatrywanej strefy na cztery elementy, kaŜdy element zawiera dwa węzły i funkcja aproksymująca będzie liniową względem osi X.

Inny sposób rozdzielenia strefy na dwa elementy z 3 węzłami powoduje wykorzystanie wielomianu aproksymującego drugiego stopnia. W tym przypadku ostatecznym wariantem aproksymacji będzie siatka z dwóch elementów skończonych drugiego stopniu.

Aproksymacja pola temperatury

Aproksymacja pola temperatury przez funkcję liniową i kwadratową


Przy opracowaniu dwu- lub trzywymiarowego modelu dyskretnego temperatury główną koncepcję MES wykorzystuje się w sposób analogiczny.

Funkcje elementów dla zadania dwuwymiarowego pokazane są na rysunku.

2.2 Dyskretyzacja ośrodka dwuwymiarowego


2.3 Element jednowymiarowy Jednowymiarowy simpleks-element jest to prosty odcinek o długości L. Oznaczmy węzły literami i, j, węzłowe wartości temperatur – przez t

ii tjodpowiednie.

Funkcja aproksymująca dla tego elementu ma postać:

Xaat 21 +=Współczynniki a1 i a2 moŜna wyznaczyć za pomocąwarunków w punktach węzłowych:

jj

ii

XXprzytt

XXprzytt

==

==

Te warunki powodują następujący układ równań:

+=

+=

jj

ii

Xaat

Xaat

21

21

rozwiązanie których daje:

L

XtXta

ijji −=1

L

tta

ij −=2


Funkcji kształtu elementu jednowymiarowego

XL

tt

L

XtXtt

ijijji

−+

−=

ji

i

jt

L

XXt

L

XXt

−+

−=

Funkcje liniowe od X nazywa się funkcjami kształtu. Oznaczymy ty funkcji przez N. KaŜda funkcja kształtu powinna miecz dolny indeks dla identyfikacji węzła, do którego ona naleŜę.

L

XXN

j

i

−=

L

XXN i

j

−=

[ ]{ }tNtNtNt jjii =+=

[ ] [ ]jiNNN ={ }

=j

i

t

tt Wykresy funkcji kształtu Ni i Nj

11

=∑=

n

Nβ

β

L

XXN

j

i

−=

L

XXN i

j

−=


Ogólne właściwości funkcji kształtu

Zarówno funkcje kształtu, otrzymane powyŜej dla dwóch typów elementów, jak i funkcje kształtu dowolnego elementu skończonego mają następujące wspólne własności:

1. Suma funkcji kształtu elementu w jego dowolnym punkcie równa jest jeden.Dla elementu jednowymiarowego tą właściwość moŜna przedstawić w postaci ogólnej:

1==−

=−

+−

=+L

L

L

XX

L

XX

L

XXNN

ijij

ji

Otrzymany wynik nie zaleŜy od X, dlatego ten warunek spełniony jest dla wszystkich punktów elementu.

2. Dowolna funkcja kształtu równa jeden w odpowiednim jej węźle i równa zeru w pozostałych węzłach tego elementu. Dla elementu jednowymiarowego ta własność jest oczywista. Na przykład, dla węzła i mamy

1==−

=−

=L

L

L

XX

L

XXN

ijj

i

3. Na granicach pomiędzy elementami funkcji kształtu są ciągłe.


Zadanie 1. Określić wartość temperatury w zadanym punkcie b

Schemat do zadania 1.

ti = 110 0C, tj = 230

0C, Xb = 4 mm

Rozwiązanie:

Obliczenie funkcji kształtu w punkcie b:

Kontrola wartości funkcji kształtu:

Wartość temperatury w punkcie b:

( ) ;75.037

47=

−

−=

−

−=

ij

bjb

iXX

XXN

( ) .25.037

34=

−−

=−

−=

ij

ibb

jXX

XXN

125.075.0 =+=+ ji NN

CNtNtt jjiib

01405.575.8225.023075.0110 =+=⋅+⋅=+=


Simpleks-element dwuwymiarowy –jest to trójkąt z trzema węzłami dla aproksymacji pola temperatury (lub innej funkcji)

Rozpatrzmy numerację węzłów w kierunku przeciwnym do strzałki zegara i oznaczymy je jako i, j, k.

2.4. Element dwuwymiarowy

Kolejność numeracji węzłów w simpleks- elemencie dwuwymiarowym


Wartości współczynników α1 α2 α3 otrzymamy wychodząc z warunków w węzłach elementu:

Funkcji kształtu elementu dwuwymiarowego

Schemat do wyznaczenia funkcji kształtu w simpleks- elemencie dwuwymiarowym

++=⇒===

++=⇒===

++=⇒===

kkkkkk

jjjjjj

iiiiii

YaXaatttYYXXprzy

YaXaatttYYXXprzy

YaXaatttYYXXprzy

321

321

321

,,

,,

,,

Następnie po rozwiązaniu układu równańotrzymamy wzory dla α1, α2 i α3 :

( ) ( ) ( )[ ]kijjijkiikijkkj tYXYXtYXYXtYXYXA

−+−+−=2

11α

( ) ( ) ( )[ ]kjijikikj tYYtYYtYYA

−+−+−=2

12α

( ) ( ) ( )[ ]kijjkiijk tXXtXXtXXA

−+−+−=2

13α

kijkijikjikj

kk

jj

ii

YXYXYXYXYXYX

YX

YX

YX

A −−−++==

1

1

1

2

gdzie: А – pole elementu skończonego


{ } { }ϕϕϕϕϕ ⋅=++= T

kkjjii NNNN

( )YcXbaA

N iiii ++=2

1

( )YcXbaA

N jjjj ++=2

1

( )YcXbaA

N kkkk ++=2

1

jki

kji

jkkji

XXc

YYb

YXYXa

−=

−=

−=

kij

ikj

kiikj

XXc

YYb

YXYXa

−=

−=

−=

ijk

jik

ijjik

XXc

YYb

YXYXa

−=

−=

−=

Funkcji kształtu elementu dwuwymiarowego

{ } { }tNNtNtNttT

kkjjii ⋅=++=


Określić wartość napręŜenia w zadanym punkcie B Zadanie 2

σσσσi = 2 MPa

Xi = 0 mm

Yi= 0 mm

σσσσj = 4 MPa

Xj= 4 mm

Yj= 0.5 mm

σσσσk = 7 MPaXk= 2 mm

Yk= 5 mm

XB=2 mm

YB=1.5 mm

σσσσB = ?

kkjjii NNN σσσσ ++=

242

5.455.0

195.0254

−=−=−=

−=−=−=

=⋅−⋅=−=

jki

kji

jkkji

XXc

YYb

YXYXa

220

505

05002

−=−=−=

=−=−=

=⋅−⋅=−=

kij

ikj

kiikj

XXc

YYb

YXYXa

404

5.05.00

0045.00

=−=−=

−=−=−=

=⋅−⋅=−=

ijk

jik

ijjik

XXc

YYb

YXYXa


( )19

7

2

1=++= YcXba

AN iiii

( )19

7

2

1=++= YcXba

AN jjjj

( )19

5

2

1=++= YcXba

AN kkkk

19

1

1

1

2 =−−−++== kijkijikjikj

kk

jj

ii

YXYXYXYXYXYX

YX

YX

YX

A

119

5

19

7

19

7=++=++ kji NNN

4.394619

534

19

740

19

7

)()()(

=++=

=++= B

kk

B

jj

B

iiB NNN σσσσ

Określić wartość napręŜenia w zadanym punkcie B


Rozwiązanie zadań, w których niewiadomą jest funkcja skalarna

1. Przypływ ciepła w stanie ustalonym 2. Niestacjonarny przepływ ciepła 3. Dyfuzji składnika w ciałach stałych4. Dyfuzja w czasie krzepnięcia materiałów dwufazowych5. Przypływ ciepła w czasie krzepnięcia materiałów

( ) ( ) ( ) 0=

∂∂

−+

∂∂

∂∂

+

∂∂

∂∂

+

∂∂

∂∂

τρ

tcQ

z

ttk

zy

ttk

yx

ttk

xeffzyx

( ) ( ) ( ) 0=

∂∂

−+

∂∂

∂∂

+

∂∂

∂∂

+

∂∂

∂∂

τu

AQz

uuk

zy

uuk

yx

uuk

xzyx

u – stęŜenie (dyfuzja), wilgotność (zw. w atmosferze), temperatura ...


3. Symulacja stacjonarnych procesów cieplnych za pomocą MES

( ) ( ) ( ) 0=

∂∂

−+

∂∂

∂∂

+

∂∂

∂∂

+

∂∂

∂∂

τρ

tcQ

z

ttk

zy

ttk

yx

ttk

xeffzyx

Zjawiska cieplne zachodzące w stanie ustalonym opisuje równanie Furiera w postaci:

k - anizotropowe współczynniki przewodzenia ciepła (W/mK) w zaleŜności od temperatury t (K), Q – prędkość generowania ciepła (W/m3)

Zadanie rozwiązania równania Furiera sprowadza się do poszukiwania minimum takiego funkcjonału, dla którego równanie Furiera jest równaniem Eulera. Według rachunku wariacyjnego funkcjonał taki będzie miał postać:

dVQtz

t

y

t

x

ttkJ

V

∫

−

∂∂

+

∂∂

+

∂∂

=222

2

)(


Warunki brzegowe

Funkcja t(x,y,z) musi spełniać określone warunki brzegowe na powierzchni metalu:

- na powierzchni metalu zadana jest temperatura t;

- na powierzchni metalu zadany jest strumień cieplny q według prawa konwekcji:

( )∞−=

∂∂

+∂∂

+∂∂

ttaz

ta

y

ta

x

ttk konwzyx α)(

- na powierzchni metalu zadany jest strumień cieplny q według prawa wymiany radiacyjnej:

( )44)( ∞−=

∂∂

+∂∂

+∂∂

ttaz

ta

y

ta

x

ttk radzyx σ

σrad - współczynnik wymiany ciepła przez radiacje (W/m2K4).

αkonw - współczynnik konwekcyjnej wymiany ciepła (W/m2 K);


Warunki brzegowe w funkcjonale Bezpośrednie wprowadzenie warunków brzegowych do funkcjonału nie jest moŜliwe. W praktyce narzuca się ten warunek poprzez dodanie do funkcjonału całki w postaci:

( ) ∫∫ +− ∞

SS

qtdSdStt2

2

α

gdzie: S – powierzchnia na której zadane są warunki brzegowe.

W rezultacie otrzymujemy:

( ) ∫∫∫ +−+

−

∂∂

+

∂∂

+

∂∂

= ∞SSV

qtdSdSttdVQtz

t

y

t

x

ttkJ

2222

22

)( α


( ) ∫∫∫ +−+

∂∂

= ∞

SS

2

V

2

dS2

1dS

2dV

2

1tqtt

x

tkJ

α

Zadanie jednowymiarowe

Siatka elementów

02

2

=dx

tdk

0=+ qdx

dtk

0)( =−+ ∞ttdx

dtk α , przy X=0;

, przy X=L

Warunki brzegowi :

Podstawowe równanie :


Wybór typu aproksymacji i

elementów skończonych.

Funkcje kształtu

( ) ( ) [ ] { }ϕϕϕ

ϕ

⋅=+

=+==

NXNXN

XCCt

jjii

10


Funkcje kształtu

( ) ( ) [ ] { }ϕϕϕ

ϕ

⋅=+

=+==

NXNXN

XCCt

jjii

10

Ni przyjmuje wartość zero w kaŜdym węźle z wyjątkiem węzła i, w którym przyjmuje wartość 1.

ij

ij

XX

XXN

−−

=

;ij

j

iXX

XXN

−

−=


[ ]∫∫ ∞−++

=VV

dSttqtdVdx

dtkJ 2

21

2

)(2

α

2)1(

21)1(

1)1( tNtNt +=

3)2(

32)2(

2)2( tNtNt +=

.

;

L

XXN

L

XXN

i

j

j

i

−=

−=

[ ] {}tNNtNtt jjii ⋅=+=

( )11)1(

1L

XXN

−=( )1

2)1(2

L

XXN

−=

( )22)2(

2L

XXN

−=

)2(3)2(

3L

XXN

−=

Zastosowanie metody elementów skończonych

Funkcje kształtu:


∫ =1

11)(s

SqtdSxqt

)1(21

)1( )(

L

tt

dx

dt +−=

)2(32

)2( )(

L

tt

dx

dt +−=

[ ]∫∫ ∞−++

=SV

dSttqtdVdx

dtkJ 2

21

2

)(2

α

[ ] ( )23

23

32

2)(

23

∞∞∞ +−=−∫ ttttS

dStxtS

αα

( ) 2322

2212

2

2 )()(2

)2()2(

1

)1()1(

ttttdVLSK

V

LSK

dxdtK +−++−=∫

Obliczenie składowych funkcjonału


)2(2

)2()2(

23

23

311

2332

222

2221

212

)2()1(

∞∞ +−+

++−++−=

ttttS

tqS

ttttttttJ CC

α

)2(

)2()2()2(

)1(

)1()1()1(

L

KSC

L

KSC

=

=

W rezultacie otrzymujemy funkcjonał:


( )

( )

=−++−=∂∂

=−++−=∂∂

=+−=∂∂

∞ 0

0

0

3)2(

2)2(

3

3)2(

2)2()1(

1)1(

2

2)1(

1)1(

1

AttACtCt

J

tCtCCtCt

J

qStCtCt

J

αα

−

=

+ −

− + −

−

∞ αSt

qS

t

t

t

α C C

C C C C

C C

0

0

0

3

2

1

) 2 ( ) 2 (

) 2 ( ) 2 ( ) 1 ( ) 1 (

) 1 ( ) 1 (

Minimalizacja funkcjonału sprowadza się do obliczenia pochodnych cząstkowych tego funkcjonału względem wartości

węzłowych temperatury:

[ ]{ } { } 0=+ PtH


Zadanie

K =75 W/cm0С,

αααα = 10 W/cm2 0С, S = 1 cm2,

L = 7.0 cm,

L1= 3.5 cm,

L2= 3.5 cm,

q = -150 W/cm2,t∞∞∞∞= 40 0С

=

−

−−

−

400

0

150

30200

204020

02020

3

2

1

t

t

t

t={70, 62.5 , 55}

C(1)= 75 / 3.5 = 20 = C(2)

ααααS(3) = 10

-qS(1) = -(-150) = 150

ααααS(3) t∞∞∞∞= 10 40 = 400


Symulacja stacjonarnych procesów cieplnych za pomocą MES. Ogólne zasady.

( ) ( ) ( ) 0=+

∂∂

∂∂

+

∂∂

∂∂

+

∂∂

∂∂

Qz

ttk

zy

ttk

yx

ttk

xzyx

Zjawiska cieplne zachodzące w stanie ustalonym opisuje równanie Furiera w postaci:

dVQtz

t

y

t

x

ttkJ

V

∫

−

∂∂

+

∂∂

+

∂∂

=222

2

)(

( ) ∫∫∫ +−+

−

∂∂

+

∂∂

+

∂∂

= ∞SSV

qtdSdSttdVQtz

t

y

t

x

ttkJ

2222

22

)( α

Wprowadzenie warunków brzegowych:

Zadanie rozwiązania równania Furiera sprowadza się do poszukiwania minimum funkcjonału:


Dyskretyzacja przedstawionego problemu

Dyskretyzacja przedstawionego problemu polega na podzieleniu rozpatrywanej strefy na elementy i przedstawieniu temperatury wewnątrz elementu jako funkcji wartości węzłowych zgodnie z zaleŜnością:

{ } { }∑=

==n

i

T

ii tNtNt1

Wprowadzając zaleŜności t i dt/dx do funkcjonału otrzymamy:

{ } { } { } { } { } { } { } { } { } { }( ) { } { } .22

)( 2222

∫∫∫ +−+

−

∂∂

+

∂∂

+

∂∂

= ∞

S

T

S

T

V

T

TTT

dStNqdSttNdVtNQtz

Nt

y

Nt

x

NtkJ

α

{ } { }( ) { } { }tx

NtN

xx

tT

T

∂∂

=∂∂

=∂∂


Minimalizacja funkcjonału Minimalizacja funkcjonału sprowadza się do obliczenia pochodnych cząstkowych tego funkcjonału względem wartości węzłowych temperatury, Ŝe w rezultacie prowadzi do następującego układu równań:

{ }{ } { } { } { } { } { } { } { } { } { }( ){ } { } .)( ∫∫∫ +−+

−

∂∂

∂∂

+

∂∂

∂∂

+

∂∂

∂∂

=∂∂

∞

SS

T

V

TTT

dSNqdSNttNdVNQtz

N

z

N

y

N

y

N

x

N

x

Ntk

t

Jα

Ten układ równań zapisany w postaci macierzowej ma postać:

[ ]{ } { } 0=+ PtH

[ ] { } { } { } { } { } { } { }{ } ,)( ∫∫ +

∂∂

∂∂

+

∂∂

∂∂

+

∂∂

∂∂

=S

T

V

TTT

dSNNdVz

N

z

N

y

N

y

N

x

N

x

NtkH α

{ } { } { }∫ ∫−−= ∞

S V

dVNQdStNP .α

Minimalizacja funkcjonału moŜe być równieŜ wykonana przez bezpośredni dobór węzłowych wartości temperatury.


Symulacja niestacjonarnych procesów cieplnych za pomocą MES. Ogólne zasady.

Równanie Furiera dla procesu niestacjonarnego ma postać:

( ) ( ) ( ) 0=

∂∂

−+

∂∂

∂∂

+

∂∂

∂∂

+

∂∂

∂∂

τρ

tcQ

z

ttk

zy

ttk

yx

ttk

xeffzyx

W określonej chwili czasu pochodne temperatury mogą być traktowane jako funkcje tylko współrzędnych x,y,z. Wtedy rozwiązanie równania Furiera jest prowadzone analogicznie jak dla procesu stacjonarnego przyjmując całe wyraŜenie w nawiasie jako parametr Q.

[ ]{ } [ ] { } { } 0=+∂∂

+ PtCtHτ

[ ] { } { }∫=V

T

eff dVNcNC ρ[ ]{ } { } 0=+ PtH


Uwzględnienie czasu za pomocą metody waŜonych residuum

W ogólnym przypadku wartości temperatury w węzłach {t} zaleŜą od czasu. Przyjmując, Ŝe wektor {t0} reprezentuje temperatury węzłowe w chwili τ=0, to w przedziale czasu ∆τwektor ten będzie wyznaczony równaniem:

{ } { } { }{ }

=1

010 ,

t

tNNt

W tym równaniu {N0} i {N1} są funkcjami kształtu zaleŜnymi od czasu. Przyjmując, Ŝe dla małych przedziałów ∆τ zaleŜność temperatur węzłowych od czasu jest liniowa, funkcje kształtu przyjmą postać:

τττ

∆−∆

=0N

ττ∆

=1N

{ } { }{ }

{ } { }{ }

−∆

=

∂

∂

∂

∂=

∂∂

1

0

1

010 1,11

,t

t

t

tNNt

ττττ


Dyskretyzacja czasowaPoniewaŜ wektor temperatur węzłowych jest znany, dla przeprowadzenia całkowania równania Furiera względem czasu naleŜy wprowadzić tylko jedną waŜoną residualną zgodnie z zaleŜnością:

[ ]{ } { }{ }

{ }{ }

{ } 0,,1

010

1

010

0

1 =

+

∂∂

∂∂

+

∫∆

τττ

τ

dPt

tNNC

t

tNNHN

Wprowadzając funkcje kształtu N0 i N1 do tego równania otrzymamy:

[ ] { } { } { } { }( ) { } 01010

0

=

++−

∆+

∆+

∆−∆

∆∫∆

τττ

ττττ

τττ

dPttC

ttH

[ ] [ ] { } [ ] [ ] { } { } 0333

2 01 =+

∆

−+

∆

+ PtCt

HtCt

H

Otrzymane wyraŜenie jest układem liniowych równań algebraicznych pozwalających obliczyćwartości temperatur węzłowych {t1} po czasie ∆t przy zadanych temperaturach {t2} w chwili τ=0

[ ]{ } [ ] { } { } 0=+∂∂

+ PtCtHτ


Zagadnienie wyznaczenia nieustalonego pola temperatury we wsadzie o przekroju okrągłym

Pole temperaturowe we wsadzie o przekroju okrągłym.

Schemat obliczeniowy do wyznaczenia nieustalonego pola temperatury we wsadzie o przekroju okrągłym.


Proces minimalizacji funkcjonału dla jednego elementu

∫∫∫ ∞−+−

=SVV

dSttQtdVdVdx

dtkJ 2

21

2

)(2

α

Temperatura wewnątrz elementów zdefiniowana jest następnym wzorom:

21

12

22111

tr

rrt

r

rrtNtNtNt

nodn

i

ii ∆−

+∆−

=+==∑=

Ni– funkcji kształtu węzłów, t

1i t2– temperatury w węzłach rozpatrywanego

elementu.

Wyznaczymy pochodną temperatury względem r:r

ttt

r

Nt

r

N

r

t

∆−

=∂∂

+∂∂

=∂∂ 12

22

11


Obliczymy całkę objętościową w funkcjonale

∫∫∫ ∞−+−

=SVV

dSttQtdVdVdx

dtkJ 2

21

2

)(2

α

rLdrdV π2=

LrdSS

max2π=∫

L – długość wsadu, rmax

– promień wsadu

( )∑∫∫ ∑∫==

∆−

=

∆−

=

∂∂

=

pnodn

p

pp

r

r

r

r

n

i

ii

V

Jwrr

ttLkrdr

r

ttkLrLdrt

r

NkdV

dx

dtk

1

2

12

2

12

2

1

2

det222

2

1

2

1

πππ

gdzie: detJ – wyznacznik macierzy Jacobiego, który jest Jakobianem transformacji układu współrzędnych ( ), w – współczynniki wagi w punktach całkowania Gaussa rp


Transformacja układu współrzędnych

Dla rozpatrywanego przypadku (jednowymiarowego) transformacja wyznaczona jest następującym wzorem

( ) ( ) 2122111

12

11

2

1rrrNrNrNr

nodn

i

ii ξξ ++−=+==∑=

ξ - współrzędna lokalna

Wartość wyznacznika macierzy Jacobiego:22

detdet 122

21

1 rrrr

Nr

N

d

drJ

∆=

−=

∂∂

+∂∂

=

=

ξξξ

( ) ( )∑∑∫==

∆−∆

=

∆−

=

pp n

p

pp

n

p

pp

V

wrr

ttrLkJwr

r

ttLkdV

dx

dtk

1

2

12

1

2

12

2

2det

2ππ

( ) ( ) 2122111

12

11

2

1rrrNrNrNr pppp

n

i

iipp

nod

ξξ ++−=+==∑=


Całkowanie numeryczne i analityczne

∫∫

∆

−=

∆

− 2

1

2

1

2

12

2

12

r

r

r

r

rdrr

ttkrdr

r

ttk

( ) ( ) ;482

119

2

1

2

1 21

22

2

1

=⋅=−⋅=−⋅=∫ rrrdr

r

r

( ) ( )

( ) ( ) ( ) ( )( )

( ) 02.404.82

13577.1433.03433.0577.1

2

1

13577.011577.013577.011577.012

1

det12

11

2

1det

2

121

2

1

2

1

=⋅=⋅++⋅+

=⋅⋅++⋅−+⋅−+⋅+

=

++−== ∑∑∫==

p

p

ppp

p

ppp

r

r

JwrrJwrrdr ξξ

( ) ( ) 2122111

12

11

2

1rrrNrNrNr pppp

n

i

iipp

nod

ξξ ++−=+==∑=22

detdet 122

21

1 rrrr

Nr

N

d

drJ

∆=

−=

∂∂

+∂∂

=

=

ξξξ


Dyskretyzacja czasowaWartość współczynnika Q moŜna wyznaczyć następująco:

τρd

dtcQ =

( )( )

( ) ( )( )[ ] ,2

2

12211202101

22211

122112021012211

∑

∑∫∫

=

=

++−+∆∆

=

=∆+−−+∆

==

p

p

n

p

pp

n

p

pp

VV

wrtNtNtNtNtNtNrLc

rwrtNtNtNtNtNtNLc

tdVd

dtcQtdV

τρπ

τρπ

τρ

{ }{ } 2021010

2211

tNtNt

tNtNt

+=

+=

( ) ( )ττ ∆

+−+= 2021012211 tNtNtNtN

d

dt

{ } { }{ }

{ }{ }{ }

−∆

=

∂

∂

∂

∂=

∂∂

t

t

t

tNNt 0010 1,11

,ττττ


Dyskretyzacja ośrodka

( )22max2

21 )( ∞∞ −=−∫ ttLrdStt

S

απαLrdSS

max2π=∫

( ) ( ) ( )( )[ ] ( ) ,2

22

2max1

22112021012

22111

2

12∞

==

−+++−+∆∆

−

∆−∆

= ∑∑ ttLrwrtNtNtNtNtNtNrLc

wrr

ttrLkJ

pp n

p

pp

n

p

ppe απτρπ

π

( ) ( ) ( )( )[ ] ( ) .2

22

2max1

22112021012

22111

2

12∞

==

−+++−+∆∆

−

∆−∆

= ∑∑ ttrwrtNtNtNtNtNtNrc

wrr

ttrkJ

pp n

p

pp

n

p

ppe ατρ

=∂∂

=∂∂

0

0

2

1

t

J

t

J

e

e

Dla minimalizacji funkcjonału wykorzystamy warunek ekstremum funkcji:


Proces minimalizacji funkcjonału

( ) ( )( ) .0221

1120210112211

1

12

1

=+−+∆∆

−

∆−

∆−

∆=∂∂ ∑∑

==

pp n

p

pp

n

p

ppe wrNtNtNNtNtN

rcwr

rr

ttrk

t

J

τρ

( ) .02

44

11202101

121

12

1

21

11

1

=+∆∆

+

+

∆∆

−∆

−+

∆∆

−∆

=∂∂

∑

∑∑∑∑

=

====

p

pppp

n

p

pp

n

p

pp

n

p

pp

n

p

pp

n

p

ppe

wrNtNtNrc

wrNNrc

wrr

ktwrN

rcwr

r

kt

t

J

τρ

τρ

τρ

( ) .022

244

max1

2202101

max1

22

12

121

11

2

=−+∆∆

+

+

+

∆∆

−∆

+

∆∆

−∆

−=∂∂

∞=

====

∑

∑∑∑∑

trwrNtNtNrc

rwrNrc

wrr

ktwrNN

rcwr

r

kt

t

J

p

pppp

n

p

pp

n

p

pp

n

p

pp

n

p

pp

n

p

ppe

ατρ

ατρ

τρ

Analogiczne dla t2:

Po zróŜniczkowaniu funkcjonału względem temperatury t1 w węzłach, otrzymamy:


Równania w postaci macierzowej

=

2

1

2221

1211

2

1

P

P

HH

HH

t

t

∑∑== ∆

∆−

∆=

pp n

p

pp

n

p

pp wrNrc

wrr

kH

1

21

111

2

τρ

∑∑== ∆

∆−

∆−=

pp n

p

pp

n

p

pp wrNNrc

wrr

kH

121

112

2

τρ

∑∑== ∆

∆−

∆−=

pp n

p

pp

n

p

pp wrNNrc

wrr

kH

112

121

2

τρ

max1

22

122 2

2rwrN

rcwr

r

kH

pp n

p

pp

n

p

pp ατρ

+∆∆

−∆

= ∑∑==

( )∑=

+∆∆

−=pn

p

ppwrNtNtNrc

P1

12021011

2

τρ

( ) ∞=

++∆∆

−= ∑ trwrNtNtNrc

Ppn

p

pp max1

22021012 22

ατρ


Układ równań dla całego ośrodkaW celu otrzymania układu równań dla całego ośrodka naleŜy dodawać do elementów globalnej macierzy odpowiednie elementy lokalnej macierzy wszystkich elementów:

[ ] [ ]∑=

=en

e

eg HH1

Przystępując do budowy macierzy sztywności dla całego ośrodka naleŜy w pierwszej kolejności zmienić indeksy zgodnie z numeracją o numerach stopni swobody całego ośrodka. W tym celu konieczna jest informacja o numerach punktów węzłowych, przylegających do kaŜdego z elementów. Dla elementu numer trzy informacja taka zakodowana jest w macierzy:

Schemat podziału na elementy ilustrujący globalną i lokalną numerację węzłów


Miejsce komponentów macierzy elementu

Dla ośrodka przedstawianego na rys miejsce komponentów macierzy elementu trzeciego pokazano w tabele


Przykład opracowania oprogramowania i obliczeń

Rozpatrywane w poprzednim rozdziale zadanie przedstawione jest poniŜej w postaci oprogramowania TEMP1d, napisanej w języku FORTRAN 90. Program główny słuŜy jedynie do wczytywania danych do obliczeń z pliku DataInpTemp1d.txt. Wczytywane są następujące dane:

Rmin - promień minimalny wsadu, m

Rmax - promień maksymalny wsadu, m

AlfaAir - współczynnik konwekcyjnej wymiany ciepła (W/m2 C)

TempBegin - temperatura początkowa, C

TempAir - temperatura środowiska, C

TauMax - czas procesu, s

C - efektywne ciepło właściwe, J/(kg*C)

K - współczynnik przewodzenia ciepła, W/(mC)

Ro - gęstość metalu, kg/(m3).


Dane do obliczeń testowych

Dane do obliczeń testowych z pliku DataInpTemp1d.txt przedstawiony są poniŜej:

**************************************************************************

0.0 Rmin, m

0.05 Rmax , m

300 AlfaAir, W/m2 K;

100 TempBegin C;

1200 TempAir C;

700 C J/(kg*Ę);

7800 Ro kg/(m3);

25 K W/(mĘ)

1800 TauMax s;

**************************************************************************


Wyniki obliczenia procesu nagrzewania wsadu

Wyniki obliczenia procesu nagrzewania wsadu o przekroju okrągłym,1 – warstwa powierzchniowa, 2 – punkcie centralnym przekroju wsadu.


Zadania praktyczne Obliczyć globalną macierz układu równań dla siatki elementów, pokazanej na rys. za pomocąprogramu TEMP1d.

Dla pierwszego elementu macierz H równa jest:


Miejsce komponentów macierzy elementu pierwszego


Miejsce komponentów macierzy elementu drugiego


Macierz globalna


Rozwiązanie zadań, w których niewiadomąjest funkcja wektorowa

•Teoria plastyczności •Teoria spręŜystości •Teoria płynów


Podstawy teorii plastyczności Teoria plastycznego płynięcia metali

a) ZaleŜność między prędkościami płynięcia metalu ta prędkościami odkształceń:

( )ijjiij vv ,,2

1+=ε&

b) Równania równowagi: 0, =jijσ

c) ZaleŜność między prędkościami

odkształceń i napręŜeniami:ij

i

p

ijij εε

σσδσ &

&2

30 +=

d) Warunek stałej objętości: 00 =ε&


Warunki brzegowi


Warunki brzegowi

• S1

• S2

• S3

• S4

• P1

• P2

( )xfric

x

xfricxyfrictooly vsign

v

vvv σσστ ===−= ;

??;;0;0 ===== yxxynx vvσσσ

?;0;0 === xyxy vvσ

?;0;0 === yxxy vvσ

0;0;0 === xyyx vv σ

0;;0 =−== xytoolyx vvv σ


Teoria małych spręŜysta-plastycznych odkształceń

a) ZaleŜność między przemieszczeniami metalu ta odkształceniami:

( )ijjiij uu ,,2

1+=ε

b) Równania równowagi:

c) ZaleŜność między odkształceniami i napręŜeniami:

ij

i

p

ijij k εεσ

εδσ2

30 +=

0, =jijσ


Sformułowanie zadania teorii plastyczności przez metodęwariacyjną

Funkcjonał – jest określony, jeŜeli kaŜdej funkcji pewnej klasy odpowiada określona liczba.

Funkcjonał – to funkcja, w której role zmiennej niezaleŜnej spełniają krzywe albo funkcje.

W modelowaniu procesów plastycznej przeróbki metali energia odkształcenia plastycznego moŜna traktować jako funkcjonał zaleŜny od składowych przemieszczenia metalu ux(x,y,z), uy(x,y,z), uz(x,y,z).

Zadaniem rachunku wariacyjnego jest określenie funkcji ux(x,y,z), uy(x,y,z), uz(x,y,z), dla jakich funkcjonał (energia odkształcenia plastycznego) osiąga minimum


→≠−+= ∫ ∫ ∫ min20 0

1V V S

fricii dSudVkdVJ ττεεσ

( ) 042 421 1

20

0

≡−−−−+= ∫ ∫∫ ∫ ∫ ∫∫− −SS SS

nn

V V S S

nnfricii dSudSudSudSudVkdVJi

τττ

ε

σσστεεσ

Energia odkształcenia plastycznego (funkcjonał)


Dla teorii plastycznego płynięcia metali funkcjonał ma postać:

→≠−+= ∫ ∫ ∫ stac

V V S

fricii dSvdVdVJ 01

0 ττεσεσ &&


W innym sformułowaniu moŜna funkcjonał przedstawisz w sposób następny:

→≠−+= ∫ ∫ ∫ min20 0

1V V S

fricpenii dSvdVKdVJ ττεεσ &&

gdzie Kpen – duŜy współczynnik kary

00 →

∞→

ε&penK


Zalety metody wariacyjnej1. Mniejsi stopień pochodnych w sformułowaniu zadania brzegowego;

2. Mamy nie duŜo (15) równań, a jedne (funkcjonał);

3. Wygodne zadanie warunków brzegowych;

Problemy

1. Konieczność rozwiązania zadania wariacyjnego (określenie funkcji, dla jakich funkcjonał osiąga minimum).


Metoda Ritza

Rozwiązanie zadania wariacyjnego według metody Ritza sprowadza się do załoŜenia postaci funkcji opisujących składowe pola prędkości.

Najwygodniej jest załoŜyć, Ŝe funkcje te są wielomianami:

+++++=

+++++=

+++++=

...

...

...

243210

243210

243210

xczcycxccv

xbzbybxbbv

xazayaxaav

z

y

x


Wartość współczynników a, b, c w równaniach wyznacza się szukając minimum mocy odkształcenia uwzględniając, ze pole prędkości musi spełniaćwarunki brzegowe na obwiedni strefy odkształcenia.

Sprowadza się to do wyeliminowania części parametrów wariacyjnych poprzez warunki brzegowe, a następnie do rozwiązania układu równań powstałego przez róŜniczkowanie funkcjonału mocy względem pozostałych parametrów wariacyjnych:

=∂∂

=∂∂

=∂∂

0

0

0

i

i

i

c

J

a

J

b

J

ni ...1=


Przykład 1.4.1.

?),(

?),(

0

=

=

=

==

=

zxv

zxv

m

const

z

x

pfric

pi

y

στ

σσ

ε&


→≠−+= ∫ ∫ ∫ min02 0

1V V S

fricpenii dSvdVKdVJ ττεεσ &&

→−= ∫ ∫ minV S

fricii dSvdVJ ττεσ &

→−=−= ∫∫ ∫ min0

21

0 0

)(b

xp

h b

ip JJdSvmdzdxJ σεσ &


−

−+=

2

2

2

2

21 31

31

b

x

h

zxaxavx

−

−+=

∂∂

=2

2

2

2

21 13

1b

x

h

zaa

x

vxxε&

−

−+−=−= 2

2

2

2

21 13

1b

x

h

zaaxz εε &&


)(13

1 2

2

2

2

21 xb

x

h

zzazadzv zz ϕε +

−

−+−== ∫ &

Przy x=z=0; vx=z=0; vxx=v=vzz=0; =0; ⇒⇒⇒⇒⇒⇒⇒⇒ ϕϕϕϕϕϕϕϕ((xx)=0)=0

−+

−−=

=

−+

−−=

∂∂

+∂∂

=

2

2

222

2

22

22

2

222

2

2

12

13

21

61

2

1

2

1

h

z

b

zxa

b

x

h

zxa

b

x

h

zza

h

z

b

xxa

x

v

z

v zxxzγ

(1.4.8)

(1.4.9)


+−=

−

−+= ∫ 9

2

231

31

222

2

21

02

2

2

2

212

baba

bamdx

b

x

h

zxaxamJ p

b

p σσ

∫ ∫∫ ∫ =+−+==h b

xzxzzz

h b

ip aafdzdxdzdxJ0 0

21222

0 0

1 );(33

4γεεεεεσ &&&&&&

=∂∂

+∂∂

=∂∂

=∂∂

+∂∂

=∂∂

0

0

2

2

2

1

2

1

2

1

1

1

a

J

a

J

a

J

a

J

a

J

a

J

−=∂∂

∂∂

=∂∂

=∂∂

∂∂

=∂∂

2

2

2

2

21

2

1

2

1

2

1

21

1

1

9

7

;);(

2

;);(

bma

J

a

aaf

a

J

bm

a

J

a

aaf

a

J

p

p

σ

σ

2

2

2

2

1

2

1

026.0648.0213.0

2416.0

h

b

h

bh

bma

a

h

va tool

++=

=


Podstawowym mankamentem metody jest trudność w określeniu granicy strefy plastycznej w przypadku procesów o duŜej nierównomierności odkształcenia.

JeŜeli zastosuje się podział na większa ilość elementów i opisze pole prędkości wielomianami niŜszego stopnia, to trudności te mogą zostać wyeliminowane.

Zasada ta zrealizowana jest w metodzie elementów skończonych.


PODSTAWY METODY ELEMENTÓW SKOŃCZONYCH

-Dyskretyzacja

-Wybór pryncypia wariacyjnego

-Wybór typu aproksymacji i elementów skończonych

-Realizacja pryncypia wariacyjnego

-Uwzględnienie warunków brzegowych

-Rozwiązanie układu równań algebraicznych

-Obliczenie odkzstalcen i napręŜeń


Typy elementów skończonych


Symulacja procesów wymiany ciepła za pomocą metodąelementów skończonych


2.2. Elementy dwuwymiarowi (trójkąty)


ϕϕϕϕ = αααα1 + αααα2Х + αααα3Y

Przy Х=Хi , Y=Yi ϕϕϕϕ = ϕϕϕϕi , ⇒⇒⇒⇒ ϕϕϕϕi = αααα1 + αααα2Хi + αααα3Yi;

przy Х=Хj , Y=Yj ϕϕϕϕ = ϕϕϕϕj , ⇒⇒⇒⇒ ϕϕϕϕj = αααα1 + αααα2Хj + αααα3Yj,

przy Х=Хk, Y=Yk ϕϕϕϕ = ϕϕϕϕk , ⇒⇒⇒⇒ ϕϕϕϕk = αααα1 + αααα2Хk + αααα3Yk

( ) ( ) ( )[ ]kijjijkiikijkkj YXYXYXYXYXYXA

ϕϕϕα −+−+−=2

11

( ) ( ) ( )[ ]kjijikikj YYYYYYA

ϕϕϕα −+−+−=2

12

( ) ( ) ( )[ ]kijjkiijk XXXXXXA

ϕϕϕα −+−+−=2

13

kijkijikjikj

kk

jj

ii

YXYXYXYXYXYX

YX

YX

YX

A

−−−++=

==

1

1

1

2

Funkcje kształtu:


X

U xx ∂

∂=ε

Y

U y

y ∂

∂=ε

∂

∂+

∂

∂=

X

U

Y

U yxxy 2

1ε

kxkjxjixix NUNUNUU ++=

kykjyjiyiy NUNUNUU ++=

( )kxkjxjixi

k

xk

j

xj

i

xi

x

x bUbUbUAX

NU

X

NU

X

NU

X

U++=

∂

∂+

∂

∂+

∂

∂=

∂

∂=

2

1ε

( )kykjyjiyi

k

yk

j

yj

i

yi

y

y cUcUcUAY

NU

Y

NU

Y

NU

Y

U++=

∂

∂+

∂

∂+

∂

∂=

∂

∂=

2

1ε

( )kykjyjiyikxkjxjixi

k

yk

j

yj

i

yi

k

xk

j

xj

i

xi

yx

xy

bUbUbUcUcUcUA

X

NU

X

NU

X

NU

Y

NU

Y

NU

Y

NU

X

U

Y

U

+++++

=

∂

∂+

∂

∂+

∂

∂+

∂

∂+

∂

∂+

∂

∂=

∂

∂+

∂

∂=

4

1

2

1

2

1ε

Zadanie 2

Obliczyć komponenty odkształcenia w elemencie skończonym:


Zadanie 4 Obliczyć komponenty odkształcenia w elemencie skończonym


Uxi = 10 mm

Uyi = -1 mm

Xi = 5 mm

Yi= 3 mm

Uxj = 10 mm

Uyj = 0 mm

Xj= 5 mm

Yj= 0 mm

Uxk = 15 mm

Uyk = -0.5 mm

Xk= 10 mm

Yk= 2 mm

εεεεx εεεεy εεεεxy = ?

Obliczyć komponenty odkształcenia w elemencie skończonym

( )kxkjxjixi

k

xk

j

xj

i

xi

x

x bUbUbUAX

NU

X

NU

X

NU

X

U++=

∂

∂+

∂

∂+

∂

∂=

∂

∂=

2

1ε

( )kykjyjiyi

k

yk

j

yj

i

yi

y

y cUcUcUAY

NU

Y

NU

Y

NU

Y

U++=

∂

∂+

∂

∂+

∂

∂=

∂

∂=

2

1ε


k

yk

j

yj

i

yi

k

xk

j

xj

i

xi

yx

xy

bUbUbUcUcUcUA

X

NU

X

NU

X

NU

Y

NU

Y

NU

Y

NU

X

U

Y

U

+++++

=

∂

∂+

∂

∂+

∂

∂+

∂

∂+

∂

∂+

∂

∂=

∂

∂+

∂

∂=

4

1

2

1

2

1ε

5510

220

−=−=−=

−=−=−=

jki

kji

XXc

YYb

5105

7310

−=−=−=

=−=−=

kij

ikj

XXc

YYb

055

303

=−=−=

=−=−=

ijk

jik

XXc

YYb

15

1

1

1

2

=−−−++=

==

kijkijikjikj

kk

jj

ii

YXYXYXYXYXYX

YX

YX

YX

A


∫∫∫ ∆−+=SV

20

V

2 dSVV2

1ττσξµ VdKdHJ pen

( )ijijij

H

tHTεσδσ &

,,20

Λ+=

( ) ( ) ( ) ( )222222 63

2zxyzxyxzzyyxH ξξξξξξξξξ +++−+−+−=

1

1 ),,(−

− Λ=

p

pp

H

tHTµ

∫=Λτ

τ0

Hd3p

Tσ

=iH ε&3=

2.3.Zastosowanie MES do modelowania procesów przeróbki

plastycznej 2.3.1. Podstawowe zasady:

100

010

001

=ijδ


∑ ∫∫∑==

+==

e

e

e

e

n

i

epenee

n

i

e dKdHJJ1 V

20

V

2

1

VV2

1ξµ

2.3.2. Przykłady obliczeń (spęczanie)

Dyskretyzacja ośrodka lepkoplastycznego:


X1=-1 Y1=1

X2=1 Y2=1

X3=1 Y3=0

X4=1 Y4=-1

X5=-1 Y5=-1

X6=-1 Y6=0

X7=0 Y7=0

Status1 = 1

Status2 = 1

Status3 = 0

Status4 = 1

Status5 = 1

Status6 = 0

Status7 = 0

nh=7n

e=6

nop(1,1)=1; nop(2,1)=7; nop(3,1)=2;

nop(1,2)=7; nop(2,2)=3; nop(3,2)=2;

nop(1,3)=3; nop(2,3)=7; nop(3,3)=4;

nop(1,4)=7; nop(2,4)=5; nop(3,4)=4;

nop(1,5)=7; nop(2,5)=6; nop(3,5)=5;

nop(1,6)=6; nop(2,6)=7; nop(3,6)=1.

Vx(1)=0; Vy(1)=Vup;

Vx(2)=0; Vy(2)=Vup;

Vx(3)=0; Vy(3)=0;

Vx(4)=0; Vy(4)=Vdown;

Vx(5)=0; Vy(5)=Vdown;

Vx(6)=0; Vy(6)=0;

Vx(7)=0; Vy(7)=0 ;

Dyskretyzacja ośrodka lepkoplastycznego:


( ) →

+== ∑ ∫∫∑

== yx

e

e

e

e VV

n

i

epenee

n

i

e dKdHJJ,

min1 V

20

V

2

1

VV2

1ξµ

kxkjxjixix NVNVNVV ++=

kykjyjiyiy NVNVNVV ++=

( )kxkjxjixi

k

xk

j

xj

i

xi

x

x bVbVbVAX

NV

X

NV

X

NV

X

V++=

∂

∂+

∂

∂+

∂

∂=

∂

∂=

2

1ξ

( )kykjyjiyi

k

yk

j

yj

i

yi

y

y cVcVcVAY

NV

Y

NV

Y

NV

Y

V++=

∂

∂+

∂

∂+

∂

∂=

∂

∂=

2

1ξ


k

yk

j

yj

i

yi

k

xk

j

xj

i

xi

yx

xy

bVbVbVcVcVcVA

X

NV

X

NV

X

NV

Y

NV

Y

NV

Y

NV

X

V

Y

V

+++++

=

∂

∂+

∂

∂+

∂

∂+

∂

∂+

∂

∂+

∂

∂=

∂

∂+

∂

∂=

4

1

2

1

2

1ξ

( ) ( ) ( ) ( )2222 63

2xyxyyxH ξξξξξ +++−=

20yx ξξ

ξ+

=

Obliczenie funkcionalu:


(((( ))))∑∑∑∑∑∑∑∑========

++++========e

e

e

e

n

i

eepeneee

n

i

e AKAHJJ1

2

0

2

1 2

1ξξξξµµµµ

1000...1

1

=

=

pen

e

K

µ

kijkijikjikj

kk

jj

ii

e

YXYXYXYXYXYX

YX

YX

YX

A

−−−++=

==

1

1

1

2

Całkowanie

funkcionalu:


program MES_1;

{

Учебная программа по курсу

«Метод конечных элементов»

Автор – профессор Миленин А.А.

CopyRight 2002

[email protected]

}

USES Crt,Printer;

CONST

nh=7; { Число узлов сетки }

ne=6; { Число конечных элементов сетки }

dVel=0.0001;

{ Малое приращение скорости }

VAR

Vx : array[1..nh] of real; { Массив скорости Vx }

Vy : array[1..nh] of real; { Массив скорости Vy }

X : array[1..nh] of real; { Массив координат узлов X }

Y : array[1..nh] of real; { Массив координат узлов Y }

Ex : array[1..ne] of real; { Массив скорости деформации Ex }

Ey : array[1..ne] of real; { Массив скорости деформации Ey }

Exy : array[1..ne] of real; { Массив скорости деформации Exy }

Ei : array[1..ne] of real; { Массив интенсивности скорости деформации Ei }

Sx : array[1..ne] of real; { Массив напряжений Sx }

Sy : array[1..ne] of real; { Массив напряжений Sy }

Sxy: array[1..ne] of real; { Массив напряжений Sxy }

S0: array[1..ne] of real; { Массив среднего напряжения S0 }

Status : array[1..nh] of integer; { Массив статусов узлов }

nop: array[1..3,1..ne] of integer; { Массив –список узлов каждого элемента }

Kpen,M : real; { Штрафной множитель и вязкость металла }

Exe,Eye,Exye,Sxe,Sye,Sxye : real;

Ae,bi,ci,bj,cj,bk,ck : real; { Площадь элемента е и коэффициенты }

Xi,Yi,Xj,Yj,Xk,Yk : real; { Координаты узлов элемента е }

Vxi,Vyi,Vxj,Vyj,Vxk,Vyk : real; { Скорости узлов элемента е }

Je,Eie,E0e,S0e : real; { Значение функционала элемента е и др. параметры}

JPrev, JNext, Jsum : real; { Вспомогательные переменные }

Jp : real;

ie,ih : integer;

Vxih,Vyih,Vtool : real;

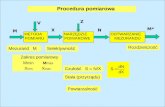
Programna

realizacja


BEGIN

{ Начало главной программы }

ClrScr;

InputData;

REPEAT{ Начало итераций по минимизации }

Funkcional;

Jp:=Jsum;

for ih:=1 to nh do begin{ Начало цикла по узлам }

if (Status[ih]=0) then begin{ Проверка статуса }

Vxih := Vx[ih];

Vyih := Vy[ih];

Funkcional;{ Расчет функционала (4.75) }

Jprev := Jsum;

Vx[ih] := Vxih + dVel;{ Приращение скорости }

Funkcional;{ Расчет функционала (4.75) }

if (Jprev<Jsum) then Vx[ih] := Vxih - dVel;{ Проверка – возрастает или убывает функционал }

Funkcional;

Jprev := Jsum;

Vy[ih] := Vyih + dVel;

Funkcional;if (Jprev<Jsum) then Vy[ih] := Vyih - dVel;

end;

end;

Funkcional;

GoToXY(30,10);

WriteLn('Funkcional = ', Jp:10:6, ' MPa*m2 ');

UNTIL (abs(Jp-Jsum)<=0.000001);

ClrScr;

{ Вывод результатов расчета }

WriteLn(' Velosity in nodes of FE grid, mm/s');

WriteLn(' ==========================');

WriteLn(' I i I Vx I Vy I');

for ih:=1 to nh do begin WriteLn(' I ' ,ih, ' I ', Vx[ih]:7:4, ' I ',Vy[ih]:7:4,' I '); end;

WriteLn(' ==========================');

ReadLn;

ClrScr;

WriteLn(' Strains in finite elements 1/s);

WriteLn(' =========================');

WriteLn(' I ie I Ex I Ey I');

for ie:=1 to ne do begin WriteLn(' I ',ie,' I ', Ex[ie]:6:4, ' I ',Ey[ie]:6:4,' I '); end;

WriteLn(' =========================');

ReadLn;

ClrScr;

WriteLn(' Stress in finite elements, MPa');

WriteLn(' ==========================');

WriteLn(' I ie I Sx I Sy I');

for ie:=1 to ne do begin WriteLn(' I ',ie,' I ', Sx[ie]:7:4, ' I ',Sy[ie]:7:4,' I '); end;

WriteLn(' ==========================');

ReadLn;

END.

Program główny


PROCEDURE InputData;

{ Процедура ввода исходных данных }

BEGIN

M:= 1;

Kpen := 100;

Vup:= - 0.1;

Vdown:= 0.1;

X[1] :=-1; Y[1] := 1; Status[1]:=1; Vx[1]:=0; Vy[1]:= Vup;

X[2] := 1; Y[2] := 1; Status[2]:=1; Vx[2]:=0; Vy[2]:= Vup;

X[3] := 1; Y[3] := 0; Status[3]:=0; Vx[3]:=0; Vy[3]:=0;

X[4] := 1; Y[4] :=-1; Status[4]:=1; Vx[4]:=0; Vy[4]:= Vdown;

X[5] :=-1; Y[5] :=-1; Status[5]:=1; Vx[5]:=0; Vy[5]:= Vdown;

X[6] :=-1; Y[6] := 0; Status[6]:=0; Vx[6]:=0; Vy[6]:=0;

X[7] := 0; Y[7] := 0; Status[7]:=0; Vx[7]:=0; Vy[7]:=0;

nop[1,1]:=1; nop[2,1]:=7; nop[3,1]:=2;

nop[1,2]:=7; nop[2,2]:=3; nop[3,2]:=2;

nop[1,3]:=3; nop[2,3]:=7; nop[3,3]:=4;

nop[1,4]:=7; nop[2,4]:=5; nop[3,4]:=4;

nop[1,5]:=7; nop[2,5]:=6; nop[3,5]:=5;

nop[1,6]:=6; nop[2,6]:=7; nop[3,6]:=1;

END;

Program

InputData


Ae := Xj*Yk + Xi*Yj + Yi*Xk - Yi*Xj - Yj*Xk - Xi*Yk;

Exe := (bi*Vxi + bj*Vxj + bk*Vxk)/(2*Ae);

Eye := (ci*Vyi + cj*Vyj + ck*Vyk)/(2*Ae);

Exye:=(bi*Vyi + bj*Vyj + bk*Vyk + ci*Vxi + cj*Vxj + ck*Vxk )/(4*Ae);

Eie:=(2.0/3.0) * sqrt( Exe*Exe + Eye*Eye - 2*Exe*Eye + 6*Exye*Exye );

E0e := 0.5*(Exe+Eye);

S0e := E0e*K;

Sxe := S0e + 1.5*Gs*(Exe-E0e);

Sye := S0e + 1.5*Gs*(Eye-E0e);

Sxye := 1.5*Gs*Exye;

Je := 0.5*M*Eie*Eie*abs(Ae) + Kpen*E0e*E0e*abs(Ae);

{ Расчет функционала по формулам (4.75) }

Jsum := Jsum + Je;

Ex[ie]:=Exe;

Ey[ie]:=Eye;

Exy[ie]:=Exye;

Ei[ie]:=Eie;

Sx[ie]:=Sxe;

Sy[ie]:=Sye;

Sxy[ie]:=Sxye;

S0[ie]:=S0e;

end;

END;

PROCEDURE Funkcional;

BEGIN

Jsum:=0;

for ie:=1 to ne do begin

Xi := X[ nop[1,ie] ];

Yi := Y[ nop[1,ie] ];

Xj := X[ nop[2,ie] ];

Yj := Y[ nop[2,ie] ];

Xk := X[ nop[3,ie] ];

Yk := Y[ nop[3,ie] ];

Vxi := Vx[ nop[1,ie] ];

Vyi := Vy[ nop[1,ie] ];

Vxj := Vx[ nop[2,ie] ];

Vyj := Vy[ nop[2,ie] ];

Vxk := Vx[ nop[3,ie] ];

Vyk := Vy[ nop[3,ie] ];

bi:=Yj-Yk;

ci:=Xk-Xj;

bj:=Yk-Yi;

cj:=Xi-Xk;

bk:=Yi-Yj;

ck:=Xj-Xi;

Program

Funkcional


Vx(1)=0; V

y(1)= -0.1000;

Vx(2)=0; V

y(2)= -0.1000;

Vx(3)= 0.0967; V

y(3)= -0.0001;

Vx(4)=0; V

y(4)= 0.1000;

Vx(5)=0; V

y(5)= -0.0001;

Vx(6)= -0.0967; V

y(6)=0;

Vx(7)=0; V

y(7)=0.

1000

1

=

=

pen

e

K

µ

Wyniki symulacji


Wyniki symulacji prezes inne oprogramowanie


Adaptacja siatki elementów


Elementy wyŜszego stopnia

x

Vxxx

i

p

x ∂∂

=+= εεεσ

σσ &&&

;2

3

1. Błąd aproksymacji

2. Błąd róŜnickowanja

3. Locking

DOF = 2*10+7=27

Ncond = ne = 30

DOF<Ncond

jS∆ ∑∆=∆jN

jSS


Element czworokąty

xyyx 4321 ααααϕ +++=

114131211 yxyx ααααϕ +++=

224232212 yxyx ααααϕ +++=

334333213 yxyx ααααϕ +++=

444434214 yxyx ααααϕ +++=

44332211 ϕϕϕϕϕ NNNN +++=

Funkcje kształtu ?

consty

constx

≠∂∂

≠∂∂

ϕ

ϕ


ϕϕϕϕ = αααα1 + αααα2Х + αααα3Y

Przy Х=Хi , Y=Yi ϕϕϕϕ = ϕϕϕϕi , ⇒⇒⇒⇒ ϕϕϕϕi = αααα1 + αααα2Хi + αααα3Yi;

przy Х=Хj , Y=Yj ϕϕϕϕ = ϕϕϕϕj , ⇒⇒⇒⇒ ϕϕϕϕj = αααα1 + αααα2Хj + αααα3Yj,

przy Х=Хk, Y=Yk ϕϕϕϕ = ϕϕϕϕk , ⇒⇒⇒⇒ ϕϕϕϕk = αααα1 + αααα2Хk + αααα3Yk

( ) ( ) ( )[ ]kijjijkiikijkkj YXYXYXYXYXYXA

ϕϕϕα −+−+−=2

11

( ) ( ) ( )[ ]kjijikikj YYYYYYA

ϕϕϕα −+−+−=2

12

( ) ( ) ( )[ ]kijjkiijk XXXXXXA

ϕϕϕα −+−+−=2

13

kijkijikjikj

kk

jj

ii

YXYXYXYXYXYX

YX

YX

YX

A

−−−++=

==

1

1

1

2

Funkcje kształtu:


Element prostokątny

ab

a

b

4

4

4

4

43214

43213

43212

43211

ϕϕϕϕα

ϕϕϕϕα

ϕϕϕϕα

ϕϕϕϕα

−+−=

++−−=

−++−=

+++=




44332211 ϕϕϕϕϕ NNNN +++=

( )( )yaxbab

N −−=4

11

( )( )yaxbab

N −+=4

12

( )( )yaxbab

N ++=4

13

( )( )yaxbab

N +−=4

14

Funkcje kształtu

( )( )yaxbab

N −−=4

11


( )( ) ( )( )ηξ −−=

−

−=−−= 114

111

4

1

4

11

a

y

b

xyaxb

abN

( )( ) ( )( )ηξ −+=

−

+=−+= 114

111

4

1

4

12

a

y

b

xyaxb

abN

( )( ) ( )( )ηξ ++=

+

+=++= 114

111

4

1

4

13

a

y

b

xyaxb

abN

( )( ) ( )( )ηξ +−=

+

−=+−= 114

111

4

1

4

14

a

y

b

xyaxb

abN

Funkcje kształtu


Odbicie (przekształcenie)


Formuły przekształcenia :

θθ

sin

cos

ry

rx

=

=


ηηη

ξξξ

∂∂

∂∂

+∂∂

∂∂

=∂∂

∂∂

∂∂

+∂∂

∂∂

=∂∂

y

y

Nx

x

NN

y

y

Nx

x

NN

iii

iii

∂∂∂∂

=

∂∂∂∂

y

Nx

N

JN

N

i

i

i

i

η

ξ

∂∂

∂∂

∂∂

∂∂

=

ηη

ξξyx

yx

J

∂∂∂∂

=

∂∂∂∂

−

η

ξi

i

i

i

N

N

J

y

Nx

N

1

∂∂

∂∂

−

∂∂

−∂∂

=−

ξη

ξηxx

yy

JJ

det

11

∫ ∫∫− −

=1

1

1

1

detdxdy ηξdJdS

Obliczenie pochodnych:


4433221

11 xNxNxNxNxNxnodesN

i

ii +++== ∑=

4433221

11 yNyNyNyNyNynodesN

i

ii +++== ∑=

Przekształcenie izoparametriczne (1-go stopnia)

( )( )ηξ −−= 114

11N

( )( )ηξ −+= 114

12N

( )( )ηξ ++= 114

13N

( )( )ηξ +−= 114

14N


Zadanie 1

X1 = 1 mm

Y1 = 1 mm

X2 = 3 mm

Y2 = 1 mm

X3 = 4 mm

Y3 = 4 mm

X4 = 0.5 mm

Y4 = 4 mm

ξξξξB=0.5ηηηηB=0.5

XB, YB = ?

( )( )16

111

4

11 =−−= ηξN

( )( ) ( )( )16

35.015.01

4

111

4

12 =−+=−+= ηξN

( )( ) ( )( )16

95.015.01

4

111

4

13 =++=++= ηξN

( )( ) ( )( )16

35.015.01

4

111

4

14 =+−=+−= ηξN


2.593755.016

34

16

93

16

31

16

1443322

111 =+++=+++== ∑

=

xNxNxNxNxNxnodesN

i

iiB

3.25416

34

16

91

16

31

16

1443322

111 =+++=+++== ∑

=

yNyNyNyNyNynodesN

i

iiB

116

3

16

9

16

3

16

14321 =+++=+++ NNNN



σσσσ1 = 40 MPa

X1 = 1 mm

Y1 = 1 mm

σσσσ2 = 34 MPa

X2 = 3 mm

Y2 = 1 mm

σσσσ3 = 46 MPaX3 = 4 mm

Y3 = 4 mm

σσσσ4 = 32 MPaX4 = 0.5 mm

Y4 = 4 mm

ξξξξB=0.5ηηηηB=0.5

σσσσB , XB, YB = ?

40.7516

332

16

946

16

334

16

140

44332211

=+++

=+++= NNNNB σσσσσ

( )( )16

111

4

11 =−−= ηξN

( )( ) ( )( )16

35.015.01

4

111

4

12 =−+=−+= ηξN

( )( ) ( )( )16

95.015.01

4

111

4

13 =++=++= ηξN

( )( ) ( )( )16

35.015.01

4

111

4

14 =+−=+−= ηξN

2.593755.016

34

16

93

16

31

16

1443322

111 =+++=+++== ∑

=

xNxNxNxNxNxnodesN

i

iiB

3.25416

34

16

91

16

31

16

1443322

111 =+++=+++== ∑

=

yNyNyNyNyNynodesN

i

iiB



σσσσ1 = 40 MPaX1 = 1 mmY1 = 1 mm



σσσσ4 = 32 MPaX4 = 0.5 mmY4 = 4 mm

XB=2.5YB=3.25

σσσσB , ξξξξ B, ηηηη B = ?

44332211 NNNNB σσσσσ +++=

( )( )ηξ −−= 114

11N

( )( )ηξ −+= 114

12N

( )( )ηξ ++= 114

13N

( )( )ηξ +−= 114

14N

2.54433221

11 =+++== ∑=

xNxNxNxNxNxnodesN

i

iiB

3.254433221

11 =+++==∑=

yNyNyNyNyNynodesN

i

iiB


( )( ) ( )( ) ( )( ) ( )( )

( ) ( ) ( )[ ]4321432143214321

43214433221

11

4

1

114

111

4

111

4

111

4

1

xxxxxxxxxxxxxxxx

xxxxxNxNxNxNxNx

BBBB

BBBBBBBB

N

i

iiB

nodes

−+−+−++−+++−−++++=

=+−++++−++−−=+++== ∑=

ηξξη

ηξηξηξηξ

( )( ) ( )( ) ( )( ) ( )( )

( ) ( ) ( )[ ]4321432143214321

43214433221

11

4

1

114

111

4

111

4

111

4

1

yyyyyyyyyyyyyyyy

yyyyyNyNyNyNyNy

BBBB

BBBBBBBB

N

i

iiB

nodes

−+−+−++−+++−−++++=

=+−++++−++−−=+++== ∑=

ηξξη

ηξηξηξηξ

( ) ( ) ( )[ ] ( ) ( ) ( )[ ]5.15.55.05.84

15.04315.04315.04315.0431

4

15.2 BBBBBBBB ηξξηηξξη +++=−+−+−++−+++−−++++=

( ) ( ) ( )[ ] [ ]BBBBBBBB ηξξηηξξη 006104

14411441144114411

4

125.3 +++=−+−+−++−+++−−++++=


( ) ( ) ( )[ ] ( ) ( ) ( )[ ]5.15.55.05.84

15.04315.04315.04315.0431

4

15.2 BBBBBBBB ηξξηηξξη +++=−+−+−++−+++−−++++=

( ) ( ) ( )[ ] [ ]BBBBBBBB ηξξηηξξη 006104

14411441144114411

4

125.3 +++=−+−+−++−+++−−++++=

5.06

1025.34=

−⋅=Bη

[ ]75.075.225.05.84

15.2 BB ξξ +++=

357.05.3

75.85.24=

−⋅=Bξ

44332211 NNNNB σσσσσ +++=


Typy elementów skończonych (2-go stopnia)


Typy elementów skończonych (2-go stopnia)

( )( )( )

( )( )

( )( )( )

( )( )ξη

ηξηξ

ηξ

ηξηξ

+−=

−−−+=

−−=

++−−−=

112

1

1114

1

112

1

1114

1

24

3

22

1

N

N

N

N

( )( )( )

( )( )

( )( )( )

( )( )ξη

ηξηξ

ηξ

ηξηξ

−−=

+−+−−=

+−=

−+++=

112

1

1114

1

112

1

1114

1

28

7

26

5

N

N

N

N


( )( )( )

( )( )

( )( )( )

( )( )ξη

ηξηξ

ηξ

ηξηξ

+−=

−−−+=

−−=

++−−−=

112

1

1114

1

112

1

1114

1

24

3

22

1

N

N

N

N

( )( )( )

( )( )

( )( )( )

( )( )ξη

ηξηξ

ηξ

ηξηξ

−−=

+−+−−=

+−=

−+++=

112

1

1114

1

112

1

1114

1

28

7

26

5

N

N

N

N

∑=

=nodesN

i

iixNx1

∑=

=nodesN

i

ii yNy1

Przekształcenie izoparametriczne(2-go stopnia)


Dyskretyzacja ośrodka za dopomogę przekształcenia 2-go

stopnia:


∂∂

∂∂

∂∂

∂∂

=

ηη

ξξyx

yx

J

∑

∑

=

=

=

=

nodes

nodes

N

i

ii

N

i

ii

yNy

xNx

1

1 ηξηξ ∂∂

∂∂

−∂∂

∂∂

=xyyx

Jdet

∫ ∫∫− −

==1

1

1

1

detdxdy ηξdJdSS

Określić pole elementu

X1 = 1 mm

Y1 = 1 mm

X2 = 3 mm

Y2 = 1 mm

X3 = 4 mm

Y3 = 4 mm

X4 = 0.5 mm

Y4 = 4 mm ( )( )ηξ −−= 114

11N

( )( )ηξ −+= 114

12N

( )( )ηξ ++= 114

13N

( )( )ηξ +−= 114

14N


Określić pole elementu

( )( )ηξ −−= 114

11N

( )( )ηξ −+= 114

12N

( )( )ηξ ++= 114

13N

( )( )ηξ +−= 114

14N

( )( ) ( )( )

( )( ) ( )( )

( ) ( ) ( )

( )

+−+

+

++

−+

−−=

=

+−∂

+

++∂

+

+

−+

∂+

−−

∂=

∂∂

η

ηηη

ηξξ

ηξξ

ηξξ

ηξξξ

14

1

14

11

4

11

4

1

114

111

4

1

114

111

4

1

4

321

43

21

x

xxx

xx

xxx

ηξηξ ∂∂

∂∂

−∂∂

∂∂

=xyyx

Jdet44332211

1

xNxNxNxNxNxnodesN

i

ii +++== ∑=


ηξε ddUy

NU

x

NLdS

y

U

x

ULdV

nodes nodesN

i

N

i

yii

xii

S

yx

V

Jdet22

1 1

1

1

1

2

1 1

2

20 ∫ ∫ ∑ ∑∫∫

− − = =

∂∂

+∂∂

=

∂

∂+

∂∂

=

∂∂

∂∂

∂∂

∂∂

=

ηη

ξξyx

yx

J

∑

∑

=

=

=

=

nodes

nodes

N

i

ii

N

i

ii

yNy

xNx

1

1

ηξηξ ∂∂

∂∂

−∂∂

∂∂

=xyyx

Jdet

Całkowanie numeryczne funkcjonału:


ηξε ddUy

NU

x

NLdS

y

U

x

ULdV

nodes nodesN

i

N

i

yii

xii

S

yx

V

Jdet44

121

1

1

1 1 1

2

20 ∫ ∫ ∑ ∑∫∫

− − = =

∂∂

+∂∂

=

∂

∂+

∂∂

=

∂∂∂∂

=

∂∂∂∂

−

η

ξi

i

i

i

N

N

J

y

Nx

N

1

∂∂

∂∂

−

∂∂

−∂∂

=−

ξη

ξηxx

yy

JJ

det

11

∂∂

∂∂

−∂∂

∂∂

=∂∂

ξηηξyNyN

Jx

N iii

det

1

∂∂

∂∂

+∂∂

∂∂

−=∂∂

ξηηξxNxN

Jy

N iii

det

1

Całkowanie numeryczne :


∑ ∑∫∫

∫ ∫ ∑ ∑∫∫

= =− −

− − = =

==

=

∂∂

+∂∂

=

∂

∂+

∂∂

=

p p

nodes nodes

N

i

N

j

jiji

N

i

N

i

yii

xii

S

yx

V

fWWddf

ddUy

NU

x

NLdS

y

U

x

ULdV

1 1

1

1

1

1

21

1

1

1 1 1

2

20

),(),(

Jdet44

1

ηξξηηξ

ηξε

121 ==WW

Całkowanie numeryczne Gaussa:


9

89

5

2

31

=

==

W

WW

Całkowanie numeryczne Gaussa:


Przykład wykorzystania MES do optymalizacji technologii


20 MN

1 etap

technologji


50 MN

(a)


50 MN

(b)


100 MN


20 MN


50 MN

(b)


100 MN

Metoda elementów skończonychmilenin/Dydaktyka/MES/MES2005a.pdf · Metoda Elementów Skończonych...

Documents

Transcript of Metoda elementów skończonychmilenin/Dydaktyka/MES/MES2005a.pdf · Metoda Elementów Skończonych...