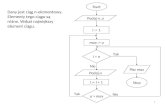
Pojęcie granicy ciągu
Click here to load reader
-
Upload
klaudia-szlagor -
Category
Documents
-
view
1.154 -
download
0
description
Transcript of Pojęcie granicy ciągu

Kolegium Nauczycielskiew Bielsku-Białej
Klaudia Brudny
Pojęcie granicy ciągu
Praca dyplomowa
napisana pod
kierunkiem naukowym
prof. dr hab. Henryka Kąkola
Bielsko-Biała 2011

Niniejsza praca dyplomowa opracowana została przeze mnie samodzielnie i zgodnie z Ustawą
o prawie autorskim i prawach pokrewnych z dnia 4.02.1994r. (Dz. U. 1994 nr 24 poz. 83) wraz
z nowelizacją z dnia 25.03.2003r. (Dz. U. 2003 nr 166 poz. 1610) oraz z dnia 1.04.2004r.
(Dz. U. 2004 nr 91 poz. 869).
Bielsko-Biała, dnia . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
czytelny podpis studenta
2

Spis treści
Wstęp …........................................................................................................................................... 4
1. Definicja granicy ciągu ......................................................................................................... 5
1.1. Przykład 1 .................................................................................................................... 5
1.2. Przykład 2 .................................................................................................................. 11
1.3. Przykład 3 .................................................................................................................. 14
Literatura .................................................................................................................................... 16
3

Wstęp
Pojęcie granicy ciągu jest jednym z podstawowych pojęć analizy matematycznej. Jest ono
definiowane następująco:
Ciąg {an} ma granicę g (albo dąży do granicy g ), jeżeli w każdym przedziale
(g−ε , g+ε) o środku w punkcie g , gdzie ε>0 , leżą prawie wszystkie wyrazy ciągu,
tj. wszystkie począwszy od pewnego wskaźnika N , który na ogół zależy od ε [1].
Tę zależność zwykle opisuje nierówność:
g−ε<an<g+ε , dla n≥N .
Obliczanie granic ciągów często bywa bardzo uciążliwe. W prostych przykładach można
wyznaczać granice, korzystając bezpośrednio z definicji. Natomiast w bardziej skomplikowanych
przypadkach do obliczania granic wykorzystuje się odpowiednie twierdzenia matematyczne.
Jednak, dla niektórych ciągów nawet zastosowanie tych twierdzeń nie wystarcza, by wyznaczyć
wartość liczbową ich granic.
Programy komputerowe i aplikacje z powodzeniem mogą wspomagać sam proces
wyznaczania granicy ciągu. Mają one tę zaletę, iż ukazują problem również graficznie. Narzędzia te
pomagają zarówno kształtować pojęcia matematyczne, jak i je zrozumieć. Urządzenia te dokonują
wszelkich obliczeń, dzięki czemu użytkownik może się skupić na obserwacji odpowiednich
wyników, by potem na ich podstawie formułować pewne hipotezy.
W swojej pracy przedstawiłam odpowiedni program komputerowy, który nie tylko pokazuje
czy zadany ciąg jest zbieżny, ale także sugeruje jaka jest wartość liczbowa granicy. Wykorzystałam
program komputerowy „Granica” [2] autorstwa Lidii Janik, Anny Hoinkis i Katarzyny Danek
oraz wirtualny kalkulator graficzny TI-83 Plus [3], które dołączam do pracy.
4

1. Definicja granicy ciągu
Ciąg {an} ma granicę g , jeżeli w każdym przedziale g− , g o środku g , gdzie ε>0 , leżą
prawie wszystkie wyrazy ciągu, tj. wszystkie począwszy od pewnego wskaźnika N .
g−ε < an < g+ε dla n≥N .
Symbolicznie możemy tę definicję zapisać następująco:
∀ε>0
∃N
∀n ≥ N
∣ an−g ∣< ε .
Jeżeli ciąg {an} ma granicę g , to mówimy, że jest on zbieżny do liczby g . I zapisujemy wtedy:
limn →∞
a n=g .
Jeśli zaś ciąg nie posiada granicy, mówimy, że jest to ciąg rozbieżny i zapisujemy:
limn →∞
a n=∞ .
Warto zaznaczyć, że jeśli granica istnieje, to jest dokładnie jedna. Ciąg nie może być zbieżny
jednocześnie do dwóch różnych granic. [4]
1.1. Przykład 1
Ciąg {1n } jest zbieżny, ponieważ jego granica jest równa 0 , co można zapisać symbolicznie:
limn →∞
1n
= 0 .
Rozstrzygnięcie zbieżności tego ciągu możemy sprowadzić do prostych rachunków. Wystarczy
podstawić kolejno n=1,2 ,3 , ... , tworząc tym samym kilka pierwszych wyrazów ciągu, a następnie
oszacować, do jakiej liczby ciąg będzie zmierzał.
I tak:
dla n=1 , otrzymamy wartość równą 11
= 1 , dla n=2 – wartość 12 , dla n=3 – wartość
13 itd.
Otrzymamy zatem ciąg wartości postaci:
11
, 12
, 13
, 14
, 15
, ... , 1100
, ... , 11000
, ... itd.
Tym sposobem wykonujemy ciąg prób matematycznych i obserwujemy wyniki. Zauważamy pewną
prawidłowość (wartości wyrazów ciągu są coraz mniejsze) oraz formułujemy hipotezę, że granicą
5

ciągu {1n} jest liczba zero. Jest to przykład wnioskowania empirycznego na gruncie materiału
matematycznego. Zatem, wnioskując empirycznie, możemy szacować, że wartości kolejnych
wyrazów tego ciągu będą położone coraz bliżej zera. To pozwala nam przypuszczać, że zero będzie
granicą tego ciągu. Jest to jednak tylko hipoteza matematyczna, która wymaga formalnego dowodu.
Zbieżność rozważanego ciągu możemy również zobrazować w układzie współrzędnych,
korzystając z odpowiedniego programu komputerowego „Granica”. Rysunek poniżej ilustruje
stronę po wybraniu opcji „Ciągi” i przykładu 9.
Program rysuje w układzie współrzędnych położenie kolejnych wyrazów danego ciągu.
Po narysowaniu wykresu, wyświetla się specjalne okno. Należy w nie wpisać przypuszczalną
granicę zadanego ciągu.
6

Po wyborze hipotetycznej wartości granicy program rysuje otoczenie wybranej liczby o ε=0,9 .
Otoczenie to można zmieniać specjalnym suwakiem znajdującym się po lewej stronie okna
wykresu.
Domyślne otoczenie ε=0,9 nie jest na tyle czytelne, aby określić zawieranie się punktów
wykresu. Program pozwala zmniejszyć wartość ε do odpowiednich rozmiarów. Dzięki temu
możemy trafniej zaobserwować poprawność wybranej granicy.
Zwężając zakres ε do 0,3 możemy zaobserwować, że tylko pierwszy wyraz tego ciągu
należy do otoczenia wyznaczonego przez ε . Stąd możemy wnioskować, że szacowanie granicy
tego ciągu było błędne.
Należy zmienić wartość szacowanej wcześniej granicy na inną. Niech to będzie liczba 0 .
Program domyślnie ustawia początkowe ε=0,9 . Z powyższej obserwacji wiemy, że to otoczenie
jest zbyt duże do wysnucia odpowiednich wniosków. Zmieńmy zatem jego wartość do mniejszej
liczby. Po zmianie ε , otrzymamy otoczenie zilustrowane poniżej.
7

Możemy zaobserwować zawieranie się punktów w otoczeniu dla ε=0,5 . Jedynie pierwszy
wyraz leży poza tym otoczeniem, wszystkie pozostałe – wewnątrz. Program pozwala zweryfikować
nasze spostrzeżenia, dzięki czemu możemy poprawnie wyznaczyć granicę danego ciągu.
Manipulowanie wartością ε przyczynia się do weryfikowania błędów w szacowaniu granicy oraz
pozwala zaobserwować, które wyrazy zawierają się w danym otoczeniu, a które do niego
nie należą.
Następnie program pyta o numer wyrazu, od którego począwszy wszystkie kolejne będą
zawarte w tym otoczeniu. Otoczeniu ε zostanie przypisana domyślnie wartość 0,9 . Dla
przejrzystości wykresu zmniejszymy ją do 0,5 .
Powyższa ilustracja obrazuje zawieranie się wyrazów ciągu {1n} w otoczeniu o promieniu ε=0,5
8

i środku w punkcie 0 . Wyraźnie możemy zaobserwować, które wyrazy zawierają się w tym
otoczeniu, a które leżą poza nim. Wystarczy wpisać numer wyrazu, od którego począwszy każdy
następny będzie należał do tego otoczenia.
Po wpisaniu odczytanej z wykresu wartości, ukazuje się nam okno z informacją
o poprawności naszej odpowiedzi.
Poprawnie oszacowana granica ciągu oraz wyznaczenie wyrazów należących do otoczenia
pozwalają sądzić, iż liczba 0 jest granicą tego ciągu. Podobnie jak poprzednio, również jest to
metoda wnioskowania empirycznego, która wymaga formalnego dowodu.
Program ilustruje definicję granicy ciągu, która mówi, że w otoczeniu (g−ε , g+ε) , gdzie
ε>0 , leżą prawie wszystkie wyrazy tego ciągu (czyli wszystkie poza skończoną ilością).
Powyższe ilustracje obrazują proces powstawania otoczenia ε . Dzięki niemu wyznaczyliśmy
wskaźnik N , o którym mówi definicja.
W otoczeniu powinny zawierać się wszystkie kolejne wyrazy ciągu począwszy od wskaźnika N ,
o który zapytał program. Jeśli wszystkie kolejne wyrazy należą do otoczenia, możemy stwierdzić,
że dążą one do pewnej stałej liczby g .
Intuicyjnie możemy przyjąć, że ciąg {1n} (przy n zmierzającym do nieskończoności), dąży
do zera. Możemy to zapisać symbolicznie:
{1n} →
n→∞0 .
9

Obie metody wyznaczenia ciągu prób matematycznych powstały w wyniku wnioskowania
empirycznego, polegającego na podstawianiu kolejnych liczb naturalnych (większych od zera)
w miejsce n , a następnie korygowaniu błędnych szacowań. I mimo iż wszystkie dotychczasowe
wnioski były słuszne, nie są one jednak wystarczające, by orzec, jaka jest granica ciągu {1n} .
Program komputerowy w sposób sugestywny pokazuje, że granica rozważanego ciągu jest
równa zero. Jest to jednak tylko hipoteza matematyczna, którą możemy wysnuć na podstawie
obserwacji powyższych obliczeń i wnioskowania empirycznego, tzn.
limn→∞
1n
= 0 .
Hipotezę tę należy udowodnić.
W dowodzie korzystam z definicji granicy ciągu
limn→∞
an = g ⇔ ∀ε>0
∃N
∀n > N
∣ an−g ∣< ε .
W naszym przypadku
limn→∞ {1
n}=0 ⇔ ∀ε>0
∃N
∀n > N
1n
< ε .
Obieramy dowolne ε>0 . Należy dobrać taki N , aby dla n>N spełniona była nierówność
1n
< ε .
Aby powyższa nierówność była spełniona, musi zachodzić warunek
1 < nε ,
a zatem, dzieląc przez obrane wcześniej ε , otrzymujemy nierówność postaci:
1ε
< n .
Biorąc N :=1ε , mamy n > N .
Z powyższej nierówności i obranego N mamy ostatecznie:
∀ε>0
∃N :=1
ε
∀n > N
1n
< ε .
10

1.2. Przykład 2W powyższym przykładzie podstawianie za n kolejnych liczb naturalnych (większych
od zera) nie powinno sprawić większych trudności. Należy jednak pamiętać, że nie wszystkie ciągi
są zadane prostym wzorem.
Weźmy na przykład ciąg postaci (−1)n⋅(1+1n) . Rozstrzygnięcie rozbieżności tego ciągu można
również sprowadzić do prostych rachunków. Podobnie jak we wcześniejszym przykładzie
wystarczy podstawić za n kolejne liczby naturalne. Utworzony w ten sposób ciąg kilku pierwszych
wyrazów pozwoli nam przypuszczać, że zadany ciąg nie posiada granicy.
Problem istnienia granicy można także zilustrować za pomocą programu komputerowego
„Granica”.
Poniższe zrzutki obrazują wartości liczbowe poszczególnych wyrazów ciągu (−1)n⋅(1+1n) .
Program rysuje kolejne wyrazy ciągu w układzie współrzędnych.
Następnie, w odpowiednim polu, należy wytypować hipotetyczną granicę ciągu. Po wpisaniu
wartości liczbowej program rysuje otoczenie (g−ε , g+ε) dla podanego przez nas g . Kolejna
zrzutka ilustruje otoczenie dla g=1 i ε=0,9 .
11

Odczytujemy z wykresu, iż granica g=1 jest błędnie przez nas oszacowana, ponieważ
nie wszystkie wyrazy zadanego ciągu należą do otoczenia (g−ε , g+ε) .
Można zatem wnioskować, że każda liczba większa od 1 oraz mniejsza od −1 nie może być
granicą tego ciągu. Poniższa ilustracja pokazuje otoczenie dla g=0 .
Otoczenie (g−ε , g+ε) o promieniu ε=0,9 jest największym z możliwych otoczeń jakie oferuje
program. Z wykresu możemy odczytać, że do tego otoczenia nie należy ani jeden wyraz ciągu. Dla
ε z przedziału 0< ε<1 jest to jeszcze bardziej widoczne.
Analizując powyższe rozumowanie, można mieć wątpliwości co do istnienia granicy ciągu
(−1)n⋅(1+1n) . Z obserwacji wynika, że żadna liczba z zakresu ∣g∣≥ 1 nie spełnia warunku
12

z definicji ani żadna liczba z przedziału (0,1) . natomiast liczba 0 byłaby granicą tego ciągu,
gdyby nie zbyt duże otoczenie (dla ε=2 otoczenie zawierałoby wszystkie wyrazy ciągu).
Definicja zakłada jednak, że dla dowolnie małego ε>0 każdy następny wyraz o większym
wskaźniku zawiera się w otoczeniu (g−ε , g+ε) .
Ostatecznie, można więc sądzić, iż ciąg (−1)n⋅(1+1n) nie posiada granicy. Zatem jest rozbieżny.
Taką odpowiedź program klasyfikuje jako poprawną, o czym świadczy poniższa ilustracja.
Program komputerowy jednoznacznie sugeruje, że zadany ciąg nie posiada granicy. Podobnie, jak
w poprzednim przypadku, rozstrzygnięcie problemu istnienia granicy wymaga formalnego dowodu.
Dla n parzystych ciąg przyjmuje postać {1+1n } . Korzystając z własności ciągu {1
n} ,
otrzymujemy:
limn→∞(1+1
n)=1 .
Dla n nieparzystych ciąg przyjmuje postać {−1−1n} , a jego granica:
limn→∞(−1−1
n)=−1 .
Z twierdzenia orzekającego, iż ciąg {an} nie może być zbieżny do dwóch różnych granic, można
stwierdzić, że ciąg (−1)n⋅(1+1n) nie posiada granicy.
13

1.3. Przykład 3
Rozpatrzmy ciąg postaci (1+1n)
n
. Dla tego ciągu również można przeprowadzić wnioskowanie
empiryczne, jak to miało miejsce w poprzednich przykładach, jednak obliczanie wartości
a3=(1+13)
3
, a4=(1+14)
4
itd. może być kłopotliwe. Możemy jednak zilustrować ten problem
graficznie, wiedząc, że program poprawnie wskaże nam wartości poszczególnych wyrazów ciągu.
Do zilustrowania ciągu wykorzystamy kalkulator graficzny. Pozwoli on wyznaczyć wartości
poszczególnych wyrazów danego ciągu oraz nakreślić ich wartości liczbowe.
Po dokonaniu odpowiednich ustawień, kalkulator graficzny rysuje poszczególne wyrazy ciągu. Ciąg
jest rosnący, o czym świadczą poniższe zrzutki ekranu kalkulatora.
Z powyższego rysunku można odczytać, że wartość a1=2 .
Wartość liczbowa dla pięćdziesiątego wyrazu tego ciągu wynosi w przybliżeniu 2,691588 .
14
Ilustracja 13

Natomiast wartość liczbowa dla wyrazu o wskaźniku pięćset wynosi około 2,7155685 .
Przybliżona wartość dla wyrazu a10000 wynosi 2,7181459 .
Analiza otrzymanych wartości dla odpowiednich wyrazów ciągu pozwala wysnuć hipotezę,
że jest to ciąg zbieżny, a jego granica w przybliżeniu wynosi 2,7181459 .
Formalny dowód zbieżności tego ciągu oraz wartość liczbową jego granicy możemy znaleźć
w literaturze. Granica tego ciągu nazywana jest w literaturze liczbą „e” i wynosi 2,71828 ... [5].
Widać więc, że przybliżona wartość granicy otrzymanej za pomocą kalkulatora graficznego różni
się nieznacznie od tej podawanej w literaturze.
15

Literatura
[1] Leja F.: Rachunek różniczkowy i całkowy, s. 33, PWN, Warszawa 1963.
[2] Danek K., Hoinkis A., Janik L.: Program komputerowy „Granica”.
[3] Wirtualny kalkulator graficzny TI-83 Plus,
www.up.krakow.pl/mat/komputery/materialy.html.
[4] Leja F.: Rachunek różniczkowy i całkowy, s. 34, PWN, Warszawa 1963.
[5] Krysicki W., Włodarski L.: Analiza matematyczna w zadaniach 1, s. 34, PWN,
Warszawa 2008
16