§17.7 薛定谔方程

1926 薛定谔 ( E. Schrodinger ) 微观粒子 低速

实际上，薛定谔方程是量子力学的一个基本假定，它

的正确性只能靠实验来检验。

处于势场V 中的非自由粒子

)()(2

)( 22

t,rt,rVm

t,rt

i vrhvh ΨΨ ⎥

⎦

⎤⎢⎣

⎡+∇−=

∂∂

薛定谔方程

⎟⎟⎠

⎞⎜⎜⎝

⎛∂∂

+∂∂

+∂∂

=∇ 2

2

2

2

2

22

zyx 拉普拉斯算符

退出返回

)(rVVr

=若势能函数V 不含时间 t

粒子的能量 E 是一个不随时间变化的常量

这时粒子处于定态，粒子的定态波函数可以写成

tiE

ert,r hvv −= )()( ψΨ

22 )()( rt,r vv ψΨ = )(rvψ 也叫做定态波函数

)()()(2

22

rErrVm

vvvh ψψ =⎥⎦

⎤⎢⎣

⎡+∇−

定态薛定谔方程退出返回

§17.8 一维定态问题

1. 一维无限深方势阱

)()()(dd

2 2

22

xExxVxm

ψψ =⎥⎦

⎤⎢⎣

⎡+−

h

)()()(2

22

rErrVm

vvvh ψψ =⎥⎦

⎤⎢⎣

⎡+∇−

V(x)

xO a

势函数

=)( xV { )0(0 ax <<

)0( ax,x ≥≤∞

退出返回

)()()(dd

2 2

22

xExxVxm

ψψψ=+−

h V(x)

xO a

(1) 时ax,x ≥≤ 0

∞→)(xV

势阱的壁无限高，在

处，势能突然增至无限大。

ax,x == 0

粒子的位置就被限制在阱内，粒子这时的状态为束缚态

的区域粒子出现的概率为零ax,x ≥≤ 0

)0(0 ax,x ≥≤=ψ退出返回

(2) 0 < x < a 时 V(x)

xO a

0)( =xV

ψψ Exm

=− 2

22

dd

2h

ψψ22

2 2dd

h

mEx

−=

022

2

=+ ψψ kdxd

22 2

h

mEk =令

)sin()( δψ += kxAx

0)( =aψ0)0( =ψ波函数连续退出返回

)sin()( δψ += kxAx V(x)

xO a

0=δ0)0( =ψ

kxAx sin)( =ψ

0)( =aψ 0sin =kaA

πnka =0sin =ka) 2 1 ( L,,n =

ank π

=

22 2

h

mEk =22

22 2h

mEa

n=

π

退出返回

) 3 2 1(2 2

222

Lh ,,,n

manEn ==

π

ank π

=kxAx sin)( =ψ

xa

nAx nnπψ sin)( =

1)(2

0=∫ dxx

a

nψ归一化条件

aAn

2=∫

a

n dxa

xnA0

22sin π 121 2 == aAn

退出返回

V(x)

xO a1ψE1

3ψE3

2ψE2

4ψE4

xa

na

xnπψ sin2)( =

) 3 2 1 ( L,,,n =

2

222

2manEn

πh=

) 3 2 1 ( L,,,n =

nE

nψ能量本征值

能量本征函数

n 量子数CAI

01 ≠E 粒子具有零点能退出返回

CAI

退出返回

2. 势垒贯穿)()()(

dd

2 2

22

xExxVxm

ψψ =⎥⎦

⎤⎢⎣

⎡+−

h

1) 梯形势

1 2

O x

U

0U=)(xV

0 0 0

0 ≥<

xUx

)()(dd

2 112

22

xExxm

ψψ =−h0<x

221

2h

mEk =0)()(dd

12112

2

=+ xkxx

ψψ

xikBexikAex 111 )( −+=ψ

退出返回

)()()(dd

2 22022

22

xExUxxm

ψψψ =+−h

0≥x

00 UE <<0)()(

dd

22222

2

=− xkxx

ψψ

1 2

O x

U

0U202

2)(2

h

EUmk −=

xkDexkCex 222 )( +−=ψ

)(2 ∞→xψ 0=D有界

xkCex 22 )( −=ψ

退出返回

1 2

O x

U

0UxikBexikAex 111 )( −+=ψ

xkCex 22 )( −=ψ

0

2

0

1

dd

dd

==

=xx xx

ψψ)0()0( 21 ψψ =

CkikBA

1

2=−CBA =+

Akik

ikC21

12−

=AkikkikB

21

21

−+

=退出返回

)()( 11

21

211

xikxik ekikkikeAx −

−+

+=ψ

xkAekik

ikx 2

21

12

2)( −

−=ψ

CAI

2) 势垒贯穿

能量为E 的粒子沿 x 轴正方向射向方势垒

00 VE <<

=)(xV）或（

）（

axxaxV≥≤

<< 0 0

0 0

退出返回

1

2

Ⅰ Ⅱ Ⅲ

Ⅰ Ⅱ Ⅲ

2

2

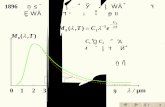
D

CT =

返回 退出

)(22

20

0 0)(16 EVma

eV

EVT

−−−≈ h

由于势垒宽度a 出现在指数上，因此穿透概率T 对a 的依赖十分敏感。

对于电子

10m10 3210 .eTa . ≈= −− ～，

10239 10 m10 −−− ≈= eTa ～，

eVEV 50 ≈−取

粒子从区域Ⅰ经区域Ⅱ到达区域Ⅲ

的穿透概率

00 VE <<

退出返回

退出返回

3) 扫描隧道显微镜 (STM)

1982宾尼(G.Binnig) 罗雷尔(H.Rohrer)

若在样品和针尖之间加一微小的电压U，可以观察到它们之间的隧道电流 I

dAUeI φ−∝

φ 样品表面平均势垒的高度

d 样品和针尖之间距离

退出返回

STM扫描图象

硅晶体表面的STM扫描图象

0 50 9030 7010 (nm)

退出返回

3. 一维谐振子

选取谐振子的平衡位置为坐标原点，并选取坐标原点为势能零点。

mk

=ω222

21

21)( xmkxxV ω==

)()()(dd

2 2

22

xExxVxm

ψψ =⎥⎦

⎤⎢⎣

⎡+−

h

0)()21(2)(

dd 22

22

2=−+ xxmEmx

xψωψ

h

退出返回

能量本征值

) 2 1 0 ()21()

21( Lh ,,,nhnnEn =+=+= νω

n•能量量子化 量子数

νh•能量间隔

•最低能量(零点能) 021

0 >= ωhE

本征函数22

21

21

)()2

()(x

nnn exH!n

xα

απ

αψ−

=21

)(h

ωα m=

厄米多项式22

)1()( ξξ

ξξ −−= e

ddeH n

nn

n

返回 退出

) 2 1 0 ()21()

21( Lh ,,,nhnnEn =+=+= νω

νnhEn=与Planck 假设不同！

E0 2/ωh=

E1 23 /ωh=

E2 25 /ωh=

E3 27 /ωh=

U(x)E

0 x CAI

退出返回

1) 经典谐振子的位置概率密度分布

能量为E0的经典

粒子沿阱壁只能爬E0高度，这时

粒子的动能为零，然后被阱壁反弹回去。

)(2 xΨ)(xU

0E

xO

在 处, 势能 021)( 22 == xmxV ω0=x , 是极小值。

动能在 处极大，则粒子通过 点时的速率也极

大，粒子在 处逗留的时间极短，出现的概率最小。

0=x 0=x0=x

退出返回

2) 量子谐振子的位置概率密度分布

能量为E0的微观

粒子沿阱壁爬的高度可以大于E0（红色虚线），或者说能量为E0的粒子可以穿入阱壁内部。

用经典理论无法解释

微观粒子分布与经典粒子分布有明显的区别

)(2 xΨ)(xU

0E

xO

20 )(xψ

2220 )( xex α

πα

ψ −=黑色实线为经典粒子位置的概率分布

退出返回

3) 谐振子的几个波函数和位置概率密度 CAI

退出返回

谐振子的定态波函数具有确定的宇称 CAI

)()( xx nn ψψ =−当 n 为偶数时 谐振子处于偶宇称态

)()( xx nn ψψ −=−当 n 为奇数时 谐振子处于奇宇称态

上述性质来源于谐振子势能函数V ( x ) 在空间反演下的不变性

)()( xVxV =−即退出返回

CAI

当n→∞时，量子概率分布→经典概率分布(图示虚线）

量子与经典的结果在平均上已比较符合

退出返回