D E S S I N S D’ E N F A N T S - Riemann...
Transcript of D E S S I N S D’ E N F A N T S - Riemann...

D E S S I N S D’ E N F A N T S:Function Theory and Algebra of Belyi
Functions on Riemann Surfaces
WithCombinatorics and Group Theory ofBelyi Functions on Riemann Surfaces
•( 1
3√2,0)
(0,0)
(1,0) •( 1
3√2,0)
(ζ3,−y3)
???????
•
(ζ23 ,y4)
•
(ζ33√2
,−y1)
???????
(ζ33√2
,y1)
???????
(ζ23
3√2,y2)
( 13√2
,0)
×(∞,∞)
(0,0)
( 13√2
,0)
•
(ζ3,y3)
??????? •(
ζ23
3√2,−y2)
(ζ2
3 ,−y4)
• (1,0)
•
by Prof. Jürgen Wolfart and Prof. Gareth Jones
in the 16th Jyväskylä Summer School24th July - 4th August 2006
Lecture Notes Taken by Tuomas Puurtinen


Contents1 Riemann Surfaces and Algebraic Curves 2
1.1 Examples . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 21.2 Important Consequences . . . . . . . . . . . . . . . . . . . . . 31.3 More Examples . . . . . . . . . . . . . . . . . . . . . . . . . . 31.4 Fact . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4
2 Introduction to Riemann Surfaces and Algebraic Curves 62.1 Alternative Approach to Riemann Surfaces of
genus 1 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7
3 Continued from Lecture 1 103.1 Why Riemann Surfaces are Projective Algebraic Curves? . . . 10
4 Belyi functions 114.1 Existence of Belyi Functions: Simple Examples . . . . . . . . 114.2 Another Example . . . . . . . . . . . . . . . . . . . . . . . . . 12
5 Continued from Lecture 2 145.1 More on Tori . . . . . . . . . . . . . . . . . . . . . . . . . . . 145.2 Alternative Approach to Finding a ”Nice” Function . . . . . . 14
6 Embeddings of Graphs, Maps and Hypermaps 166.1 Examples of Bipartite Maps . . . . . . . . . . . . . . . . . . . 166.2 More Definitions . . . . . . . . . . . . . . . . . . . . . . . . . 18
7 Uniformisation and Fuchsian Groups 207.1 Uniformisation . . . . . . . . . . . . . . . . . . . . . . . . . . 207.2 Fuchsian Groups . . . . . . . . . . . . . . . . . . . . . . . . . 22
8 Continued from Lecture 4 248.1 More on Dessins . . . . . . . . . . . . . . . . . . . . . . . . . . 248.2 Example . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 25
9 Galois Theory 269.1 Basic Galois Theory . . . . . . . . . . . . . . . . . . . . . . . 269.2 The Absolute Galois Group . . . . . . . . . . . . . . . . . . . 27
10 Continued from Lecture 5 3010.1 Remarks . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3010.2 More General Facts about Fuchsian Groups . . . . . . . . . . 30

10.3 Remarks . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 33
11 From Dessins to Holomorphic Structures 3411.1 Coverings . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3411.2 Triangle Groups and Bipartite Maps . . . . . . . . . . . . . . 3411.3 Holomorphic Structures . . . . . . . . . . . . . . . . . . . . . 3611.4 Non-cocompact Triangle Groups . . . . . . . . . . . . . . . . . 37
12 Quasiplatonic Surfaces, and Automorphisms 3912.1 Definitions and Properties . . . . . . . . . . . . . . . . . . . . 3912.2 Hurwitz Groups and Surfaces . . . . . . . . . . . . . . . . . . 4012.3 Kernels and Epimorphisms . . . . . . . . . . . . . . . . . . . . 4112.4 Direct Counting . . . . . . . . . . . . . . . . . . . . . . . . . . 4212.5 Counting by Character Theory . . . . . . . . . . . . . . . . . 43
13 Moduli Fields and Fields of Definition 45
14 Regular Embeddings of Complete Bipartite Graphs 4914.1 Regular Maps . . . . . . . . . . . . . . . . . . . . . . . . . . . 4914.2 Complete Bipartite Graphs . . . . . . . . . . . . . . . . . . . . 51
15 Generalised Fermat Curves 54
16 Some Hints Concerning Exercises 58
1

Lecture 1by Prof. Jürgen Wolfart
1 Riemann Surfaces and Algebraic CurvesRiemann surfaces are Haudorff spaces with a countable base topology, wherechart maps to C are defined with biholomorphic transition functions wherethey coincide. We are discussing here only connected Riemann surfaces.
1.1 Examples
1. Riemann sphere C = C ∪ ∞ = P1(C): Take two charts U1 and U2,for example U1
∼= C and U2∼= (C − 0) ∪ ∞. Then z 7→ 1
zis a
holomorphic mapping between the charts.
2. F affn = (x, y) ∈ C2 |xn + yn = 1 , n > 1 is a ”Fermat curve”. Take as
charts for example (x, y) 7→ y, which is homeomorphic in suitable neigh-boughoods of all points except x = 0, yn = 1, and (x, y) 7→ x which ishomeomorphic in suitable neighbourhoods of all points except y = 0,xn = 1, with transition functions x = n
√1− yn and y = n
√1− xn.
3. More general: all ”smooth” affine algebraic curves
Xaff := (x, y) ∈ C2 | f(x, y) = 0
for some polynomial f with the property that in all p ∈ Xaff
∂f
∂x(p) 6= 0 or
∂f
∂y(p) 6= 0.
The implicit function theorem says that locally around p all solutionsof f(x, y) = 0 are of the shape (h(y), y) or (x, g(x)) where h and g areholomorphic. Then the projections serve as charts.
4. Affine hyperelliptic curves: y2 = (x − a1) · . . . · (x − an) with pairwisedistinct a1, . . . , an. For example f = y2 − Π(x− ai) and we have
∂f
∂y(p) = 2y = 0
in all (ai, 0), but∂f
∂x(p) 6= 0
in these (ai, 0).
2

Theorem 1.1 Let X, Y be connected Riemann surfaces, f : X → Y non-constant holomorphic mapping, p ∈ X, f(p) = p′ ∈ Y . Then there existcharts z : U(p)→ V ⊂ C and w : U ′(p′)→ V ′ ⊂ C with z(p) = 0, w(p′) = 0such that
U
z
f // U ′
w
C : z
// w = zn : Cis commutative for some choice n ∈ N independent of the choice of the charts.The constant n = multp f is the multiplicity of f in p.
If n = 1 then f is locally biholomorphic (”unramified at p”) otherwise”ramified” of order n.
1.2 Important Consequences
1. If f : X → C is meromorphic, then if it’s non-constant, then the zerosand poles are discrete in X.
2. Ramification points of f are discrete in X.
3. Identity theorem, maximum principle, open mapping theorem are valid.
4. On compact Riemann surfaces we have for f : X → C (meromorphic,non-constant function) only a finite number of zeros or poles, and also afinite number of ramification points. Holomorphic functions f : X → Chave to be constant.
5. If f : X → Y is holomorphic and non-constant, X compact, then f issurjective and Y is compact as well.
6. Under the same hypothesis deg f :=∑
p∈f−1(y) multp f is independentof y ∈ Y .
1.3 More Examples
1. Fermat curve:
Fn := [x, y, z] ∈ P2(C) |xn + yn = zn
better (symmetric) xn + yn + zn = 0, covered by affine curves withz = 1, y = 1, x = 1. We’ll get different affine Fermat curves, when wetake charts of the form x
y, y
z, z
x. This’s a typical example of a ”smooth
3

projective algebraic curve”. Of course, because P2(C) is compact, thenFn is compact.
2. Try to compactify also hyperellictic curves
y2 = Πni=1(x− ai)⇒ y2zn−2 = Πi(x− aiz).
Now if z = 1 then we’ll have an affine curve, or if z = 0 then xn = 0and so on x = 0, normalizing by y = 1 we get affine equation
zn−2 = Π(x− ai).
Implicit function theorem isn’t applicable in situations n > 3. Here,write y2 = q(x) with
deg q =
2g + 1,
2g + 2
and withz :=
1
xand w :=
y
xg+1.
k(z) := z2g+2q
(1
z
)∈ C[z]
with deg k = 2g + 2. So then y2 = q(x) ⇔ w2 = k(z) in all pointsx 6= 0, 6= z . . ..
x = y =∞⇔ z = 0⇔
w = 0, for deg q = 2q + 1
w = ±√
k(0) for deg q = 2q + 2
1.4 Fact
Riemann surfaces are orientable! That is an implication from that the tran-sition functions are biholomorphic respecting the orientation. Surfaces canalso be triangulated: Suppose you have X triangulated. Then we have theEuler characteristic
χ(X) := f − e + v,
with f , e and v counting ”faces”, ”edges” and ”vertices”, which does not dependon the triangulation. For example χ(C) = 2 and χ(Torus) = 0.
Theorem 1.2 (Riemann-Hurwitz) If f : X → Y is non-constant holo-morphic mapping of compact Riemann surfaces, then
2g(X)− 2 = deg f(2g(Y )− 2) +∑p∈X
(multp f − 1).
4

Several applications, e.q: g(Y ) ≤ g(X) with ”=” only if f is isomorphism(unramified) or g = 1 and f is unramified. If g(X) > g(Y ) = 0 or 1, then fis ramified.
Now Fn (n>2) has genus (n−1)(n−2)2
, and we consider f : Fn → C :[x, y, z] 7→ x
z: For example z = 1, xn + yn = 1, f : (x, y) 7→ x and deg f = n.
Exceptionally, f has only one preimage in points with xn = 1: n points withmultp f = n. If then z = 0, xn + yn = 0, y = 1, n points on Fn, f has n polesand it’s unramified. Now Riemann-Hurwitz implies that
2g(Fn)− 2 = n(−2) + n(n− 1) = n2 − 3n.
Exercise 1.1 Find as many automorphisms of Fn as possible! (if possible,find 6n2 automorphisms.) Determine the structure of Aut Fn.
Exercise 1.2 Apply Riemann-Hurwitz to determine the genus of the (com-pact) hyperelliptic curves.
Theorem 1.3 There is an equivalence between the categories ”compact Rie-mann surfaces” and ”smooth projective algebraic curves”.
5

Lecture 2by Prof. Gareth Jones
2 Introduction to Riemann Surfaces and Alge-braic Curves
CompactRiemann Surfaces
oo cat.equiv.
// Smooth ProjectiveAlgebraic Curves
with maps on them oo // defined overalgebraic number fields
Galois Theory
Special case: Riemann surfaces of genus 1.
Elliptic curve: algebraic curve y2 = p(x), where p is a cubic polynomialon C[x] with distinct roots e1, e2, e3. Discriminant ∆ = 16(e1 − e2)
2(e2 −e3)
2(e3 − e1)2. Here p has distinct roots if and only if ∆ 6= 0. Applying an
affine substitution of ax + b for x we can put the equation in Weierstrassnormal form
y2 = 4x3 − c2x− c3, (c2, c3 ∈ C).
Then ∆ = c32 − 27c2
3 (easy exercise).Alternatively, applying affine substitutions to x and x, we get Legendre
normal formy2 = x(x− 1)(x− λ) (λ ∈ C\0, 1).
Exercise 2.1 Find ∆ and these normal forms for the elliptic curve
y2 = x3 − 9x2 + 23x− 15.
Now write the elliptic curve E as y =√
p(x), a 2-valued function of x.The projection (x, y) 7→ x is in general 2-to-1, showing that E is a 2-sheetedcovering of the Riemann sphere C = P1(C) = C ∪ ∞. Special cases: ifx = ej, j = 1, 2, 3, then only y = 0 is possible, and if x =∞ then only y =∞is possible. E is a branched covering of C, with branch-points at e1, e2, e3
and ∞.
6

If z = ej + reiϑ, let z rotate once around ej (but not the other roots)in the positive directions (anti-clockwise). Then
√(z − ej) is multiplied by
eiπ = −1. This means that a point (x, y) on E above x moves to (x,−y),i.e. we pass from one sheet of E to the other. The same happens if wefollow a circle around ∞, where x = reiϑ, with large constant r: each of thethree factors
√(x− ej) is multiplied by −1, and hence so is y. Construct
the Riemann surface of E by taking two copies of C (one for each branch of√p(x)), and joining them across two disjoint cuts between e1 and e2, and e3
and ∞. The result is a torus, of genus 1.
2.1 Alternative Approach to Riemann Surfaces ofgenus 1
Let ω1 and ω2 be elements of C which are linearly independent over R. Theygenerate a lattice
Λ = Λ(ω1, ω2) = mω1 + nω2 |m, n ∈ Z .
We call ω1 and ω2 a basis for Λ. Λ is a subgroup of C, and Λ is discrete(every ω ∈ Λ has an open neighbourhood containing no other element of Λ).
Define z1 ≡ z2 mod Λ if z1 − z2 ∈ Λ. Equivalence classes = cosets z + Λof Λ in C. Quotient space is then C/Λ.
The parallellogram P = xω1 + yω2 |x, y ∈ [0, 1] is a fundamentalregion for Λ, i.e. each z ∈ C is equivalent to an element of P , and if twoelements of P are equivalent, then they lie on the boundary ∂P . Form C/Λby identifying equivalent points z1, z2 ∈ ∂P . The holomorphic structure onC yields a holomorphic structure on C/Λ. Also C/Λ is a group, structureinherited from C.
To show the link between these two approaches, we need elliptic functions.These are doubly periodic meromorphic functions. Doubly periodic means
f(z + ω) = f(z) for all z ∈ C and all ω ∈ Λ.
Meromorphic: holomorphic or a pole of finite order at each point in C. Equiv-alently, f(x) =
∑∞n=k an(z − a)n near each a (Laurent series).
For a given Λ, such functions form a field F (Λ). Think of these as themeromorphic functions on C/Λ by defining f(z + Λ) = f(z) (well-defined).C/Λ is compact, so the theory of such functions works nicely.
We need some non-constant examples: Weierstrass function
℘(z) =1
z2+
∑′
ω
(1
(z − ω)2− 1
ω2
)7

where∑′
means the sum over ω 6= 0 in Λ. This is uniformly convergent oncompact subsets of C\Λ so ℘ is meromorphic, with poles of order 2 at thelattice-points. To show ℘ is double periodic, first consider
℘′(z) = −2∑
ω
1
(z − ω)3.
This is meromorphic, with poles of order 3 at the lattice-points.
Exercise 2.2 Show that ℘′ is doubly periodic with respect to Λ. Deduce that℘ is also doubly periodic (Hint: ℘ is an even function).
Thus ℘, ℘′ ∈ F (Λ) so the field C(℘, ℘′) of rational functions of ℘ and ℘′ iscontained in F (Λ). In fact, F (Λ) = C(℘, ℘′). ℘ and ℘′ are not algebraicallyindependent: they satisfy
(℘′)2 = 4℘3 − g2℘− g3,
where g2 = 60G4 and g3 = 140G6, and where Gk =∑′
ω ω−k is the Eisensteinseries. Comparing this equation with the Weierstrass normal form y2 =4x3 − c2x − c3 for E, we can write x = ℘(z), y = ℘′(z) for an appropriatelattice Λ. (Given any c2, c3 with ∆ 6= 0, one can find a lattice Λ such that g2
and g3 for Λ are equal to c2 and c3.) Identify each point (x, y) ∈ E with thecorresponding point z + Λ ∈ C/Λ. Thus we identify E with C/Λ. (Comparewith parametrising x2 +y2 = 1 by x = sin z and y = cos z, where z ∈ R/2πZ.
Suppose that Λ and Λ′ are lattices in C. The Riemann surfaces C/Λ andC/Λ′ are isomorphic (as Riemann surfaces) if and only if Λ and Λ′ are similarlattices, in the sense that Λ′ = µΛ for some µ ∈ C\0.
If Λ has basis ω1, ω2, then elements ω′1, ω′2 of Λ form a basis for Λ if and
only if ω′2 = aω2+bω1 and ω′1 = cω2+dω1 with a, b, c, d ∈ Z and ad−bc = ±1.The 2 × 2 integer matrices with ad − bc = ±1 form a group GL2(Z) undermultiplication and those with ad − bc = 1 form SL2(Z), a normal subgroup(of index 2).
The modulus τ = ω2
ω1of a basis is invariant under the similarity trans-
formation of multiplying Λ by µ. Changing basis by(
a bc d
)∈ GL2(Z)
transforms τ = ω2
ω1to
τ ′ =ω′2ω′1
=aω2 + bω1
cω2 + dω1
=aτ + b
cτ + d.
These transformations form a group PGL2(Z) ∼= GL2(Z)/±1. Transposingω1 and ω2 necessary, we can assume that Im τ > 0, i.e. τ is the upper halfplace H = τ ∈ C | Im τ > 0 .
8

This allows us to restrict to transformations τ 7→ aτ+bcτ+d
with ad− bc = 1.These form the modular group
Γ = PSL2(Z) = SL2(Z)/±I.
Then
C/Λ ∼= C/Λ′ ⇔ τ and τ ′ are equivalent under the action of Γ on H
andIsomorphism classesof elliptic curves C/Λ
oo // Orbits of Γ on H.
How does Γ act on H?For example the region F defined by |τ | ≥ 1, |Re τ | ≤ 1
2is a fundamental
region for Γ. Every orbit of Γ contains a point in F . If two points in F arein the same orbit, they lie on the boundary. The element X : τ 7→ −1
τfixes
τ = i, and this value of τ corresponds to the square lattice. The elementZ : τ 7→ τ+1 also pairs sides of F . The element Y : τ 7→ −τ−1
τfixes ω = e2πi/3
corresponding to the hexagonal lattice Λ.One can show that Γ has a presentation Γ = 〈X, Y |X2 = Y 3 = 1 〉 ∼=
C2 ∗ C3, the free product of C2 and C3.Reduction mod (n) : Z → Zn (ring-homomorphism) induces group ho-
momorphisms SL2(Z) → SL2(Zn) and hence Γ = PSL2(Z) → PSL2(Zn) =SL2(Zn)/±I.
Γ(n) := ker φn
is the principal conquence subgroup of level n.E.g. Γ(2) is a free group of rank 2, generated by τ 7→ τ
−2τ+1(fixing 0)
and τ 7→ −τ+2−2τ+3
(fixing 1).
Exercise 2.3 Show that Γ acts transitively on Q = P1(Q) = Q ∪ ∞, andthat Γ(2) has three orbits on Q. Deduce that Γ/Γ(2) ∼= S3 (symmetric groupof degree 3).
9

Lecture 3by Prof. Jürgen Wolfart
3 Continued from Lecture 1
3.1 Why Riemann Surfaces are Projective Algebraic Curves?
Sketch of ideas:
1. On a compact Riemann surface there are non-constant meromorphicfunctions f : X → C. ”⇐” by the theorem of Riemann-Roch.
2. All functions g : X → C constant on fibers of f are rational functions,in C(f). (Fiber means the points in f−1(q) for q ∈ C.)
3. Riemann-Roch: There are h : X → C separating points of the fibers off for generic q ∈ C.
4. Consider elementary symmetric combinations
S1 = h(p1) + h(p2) + . . . + h(pn), if pi = f−1(q) outside ram. pts of f,
S2 = h(p1)h(p2) + . . . + h(pn−1)h(pn)
...Sn = h(p1) · . . . · h(pn).
(1)
These are meromorphic functions on X, constant on fibers of f .
5. There exists an algebraic equation between h and f , i.e.
hn − S1hn−1 + S2h
n−2 − . . . + (−1)nSn = 0, (2)
where the left side is in C(f)[h].
6. Algebra ⇒ every meromorphic function on X lies in a field extensionC(X) of C(f) of degree at most n.
7. Function fields determine equations ⇒ use values of f and of h ascoordinates for the curve equation 2 for the curve, resolve singularitiespass to projective equation ⇒ .
10

4 Belyi functionsTheorem 4.1 Let X be a compact Riemann surface, i.e. a smooth projectivealgebraic curve from PN(C). X can be defined over Q if and only if thereexists meromorphic non-constant function β : X → C ramified above at most3 points (critical values are without loss of generality 0,1 and ∞).
There functions are called ”Belyi functions” (Belyi 1980)
4.1 Existence of Belyi Functions: Simple Examples
1. C = P1(C), β : C→ C : z 7→ z (unramified).
2. β : C→ C : z 7→ zn is ramified in z = 0 and z =∞.
3. Recall Tchebychev polynomials
T0(z) ≡ 1,
T1(z) = z,
T2(z) = 2z2 − 1
...Tn+1(z) = 2zTn(z)− Tn−1(z)
Now cos nϑ =: Tn(cos ϑ) with properties Tn : [−1, 1]→ [−1, 1], deg Tn =n, Tn has simple zeros in points cos 2k−1
2nπ, where k = 1, . . . , n and dou-
ble ±1 in between. Also simple ±1 values at points ±1. Now the squareT 2
n has double zeros, double 1-values in between, simple 1-values at ±1.Therefore T 2
n (for n > 0) is a Belyi function.
#ramification points in C = #zeros of (T 2n)′ = 2n− 1.
The picture of β−1([0, 1]) is . . . • . . . ending the bothsides with • if the zeros of β are shown as and zeros of β − 1 as •.
4. X = Fn : xn + yn = zn. Then for example β : Fn → C : [x, y, z] 7→ xn
zn .On the affine part z = 1, β : (x, y) 7→ xn, deg β = n2. Less than n2
points in β−1(xn) occur in
• points with xn = 0 ⇒ y = ζ2n (n points with β(x, y) = 0, ramifi-
cation order is n),
• points with xn = 1 ⇒ y = 0, β : (x, y) = (ζkn, 0) 7→ 1, ram. order
is n.
11

• z = 0, consider 1β
= zn
xn : take x = 1, gives n zeros, all of multp β =n.
Therefore β is a Belyi function.
A surjective Belyi function of a compact Riemann surface β : X → C in-duces a natural triangulation by β−1(R) where the preimage β−1(
0
1• )
divides X in simply connected cells. It gives a bipartite graph embedded inX, which is called ”dessin d’enfants” (by Grothendieck).
If β is a Belyi function, then also 1β, 1 − β, 1 − 1
β, 1
1−β, β
β−1are Belyi
functions. These permute the critical values 0, 1,∞.If β is a Belyi function, then also is 4β(1 − β): that’s because ∞ 7→ ∞,
0 7→ 0, 1 7→ 0, 127→ 1. Also β 7→ 4β(1− β) from C→ C is a Belyi function.
This last action induces a new bipartite graph, which can be reduced tosimpler one-colour one. This corresponds to the theory of ”maps”.
4.2 Another Example
For the construction of Belyi functions y2 = x(x−1)(x− 13√2
) elliptic functiondefined /Q. Start with (x, y) 7→ x, study ramification points: this mappingis ramified in (∞,∞), (0, 0), (1, 0), ( 1
3√2, 0). The preimage of the unit interval
in β is of following shape:
•( 1
3√2,0)
(0,0)
(1,0) •( 1
3√2,0)
(ζ3,−y3)
???????
•
(ζ23 ,y4)
•
(ζ33√2
,−y1)
???????
(ζ33√2
,y1)
???????
(ζ23
3√2,y2)
( 13√2
,0)
×(∞,∞)
(0,0)
( 13√2
,0)
•
(ζ3,y3)
??????? •(
ζ23
3√2,−y2)
(ζ2
3 ,−y4)
• (1,0)
•
12

Now(x, y) 7→ x 7→ x3 7→ 4x3(1− x3)
∞ 7→ ∞0 7→ 0
1 7→ 1
13√
27→ 1
2.
This step (using polynomials sending algebraic critical values) may inducenew ramifications, here x 7→ x3 ramified in x = 0 and x = ∞, so thecomposite (x, y) 7→ x3 is ramifield above 0, 1,∞, 1
2. The composite map will
be a Belyi function sending
(∞,∞) 7→ ∞ (pole of order 12)(0, 0) 7→ 0 (multiplicity 6)(1, 0) 7→ 0 (multiplicity 2)
(ζk3 ,±yk) 7→ 0
(13√
2, 0) 7→ 1 (multiplicity 4).
Belyi algorithm to construct β systematically: Take an equation defined/Q some function X → C, ramified above α1, . . . , αn ∈ Q. Combine witha polynomial p : C → C sending α1, . . . , αn → Q; if new ramificationsarise, repeat the procedure. . . All critical points ⊂ Q, suppose 0, 1,∞ ⊂”crit. points”. For example if 0 < m
n+m< 1 is a critical point, apply z 7→
(m+n)m+n
mnnn zn(1− z)n. Then
0 7→ 0
1 7→ 0
∞ 7→ ∞m
m + n7→ 1.
Only ramification occurs in 0, 1, mn+m
,∞.
Exercise 4.2 (continued from 2.) Find a Belyi function and a nice dessinpicture for y2 = xn − 1, n > 3.
Exercise 4.3 Find a Belyi function and a dessin for the elliptic curve
y2 = x(x− 1)(x− ζ±133√
2).
13

Lecture 4by Prof. Gareth Jones
5 Continued from Lecture 2
5.1 More on Tori
Recall the correspondence between the isomorphism classes of elliptic curvesand the orbits of Γ on H.
We would like a ”nice” function on H, taking a single value on each orbitof Γ, and different values on different orbits. We can regard g2, g3 and∆ = g3
2 − 27g23 as functions of τ ∈ H by evaluating them for the lattice
Λ = Λ(1, τ) with ω2 = τ and ω1 = 1, and with modulus τ . Difficulty: ifreplace Λ with a similar lattice Λ′ = µΛ then g2, g3 are multiplied by µ−4
and µ−6, and ∆ by µ−12. But if we define
J(τ) =g2(τ)3
∆(τ)=
g2(τ)3
g2(τ)3 − 27g3(τ)2
then the powers of µ cancel, so J(τ) depends only on the similarity classof Λ. Also, g2, g3 and hence J are independent of the basis of Λ. So J isinvariant under the action of Γ on H, i.e.
J(T (τ)) = J(τ)
for all τ ∈ H and T ∈ Γ. J is the elliptic modular function (but not anelliptic function!). J is holomorphic on H, and it induces a bijection betweenthe orbits of Γ on H and complex numbers, i.e. Γ\H↔ C.
Exercise 5.1 Evaluate J(τ) at τ = i and τ = ω = e2πi/3 and find thecorresponding elliptic curves.
5.2 Alternative Approach to Finding a ”Nice” Function
Put each elliptic curve E into Legendre form
y2 = x(x− 1)(x− λ)
where λ ∈ C\0, 1 and regard λ as a function of the modulus τ correspond-ing to E. The difficulty here is that the Legendre form for E is not quite
14

unique. This is because there are 6 ways of sending two of the three roots ofp(x) to 0 and 1, with the third going to λ, by an affine transformation.
For instance, if we replace x with 1 − x (transposing the roots 0 and 1)the right-hand side of the Legendre equation becomes
(1− x)(−x)(1− x− λ) = −x(x− 1)(x− (1− λ)).
If we also replace y with iy the left-hand side becomes −y2, so we have anisomorphic elliptic curve with Legendre form
y2 = x(x− 1)(x− (1− λ)).
Thus λ is replaced with 1−λ. Another substitution (find it!) replaces λ with1λ. These two substitutions generate a group isomorphic to S3 (corresponding
to permuting the three roots e1, e2 and e3 of p(x)), and the six permutationsgive rise to six values
λ, 1− λ,1
λ,
1
1− λ,
λ
λ− 1,λ− 1
λ.
One can define λ uniquely as a function of τ by noting that ℘′(z) = 0 atz = ω1
2and ω1+ω2
2(why?), so the differential equation
(℘′)2 = p(℘)
implies that the roots e1, e2 and e3 of p(x) are at x = ℘(ω1
2), ℘(ω2
2) and
℘(ω1+ω2
2).
An affine transformation L : x 7→ ax + b sending e2 and e3 to 0 and 1respectively sends e1 to
λ =e1 − e2
e3 − e2
and this depends only on τ . This function λ is holomorphic on H, and isinvariant under Γ(2) (a normal subgroup of index 6 in Γ), but not under Γ.The 6 cosets of Γ(2) in Γ give the 6 possible values for λ. These two functionsare related by:
J(τ) =4(1− λ(τ) + λ(τ)2)3
27λ(τ)2(1− λ(τ))2
Thus six values of λ correspond to each value of J . Then
β(x) =4(1− x + x2)3
27x2(1− x)2
is a Belyi function. It has triple zeros of β at e±2πi/6(= ζ±16 ), double zeros of
β − 1 at −1, 12, 2, and double poles of β at 0, 1,∞.
15

6 Embeddings of Graphs, Maps and Hyper-maps
Graph G = (V, E) (vertices and edges), connected, finite (relax this later),allow loops • and multiple edges • • . Map M : G → X, Xis a surface, connected, compact, without boundary, and oriented (chosenorientation counter-clockwise). The faces (connected components of X\G)must be simply-connected, i.e. homeomorphic to an open disc. Examples:Platonic solids on X = S2.
Assume that G is bipartite, i.e. we can colour the vertices black and whiteso that each edge joins a black vertex to a white vertex • (possibleiff each circuit in G has even length). Call these bipartite maps (=dessinsd’enfants) denoted by B.
6.1 Examples of Bipartite Maps
1. The dessin B1 corresponding to β is
•−1
×0
•12
~~~~~~~~
@@@@@@@@ ×1
•2
e−2πi/6
~~~~~~~~
e2πi/6
@@@@@@@@
R
Here × denotes a face-centre.
2. B2 =
•
•
Quotient of B1 by a half-turn about 12.
3. Identify opposite edges of the hexagon to get a bipartite map B3 on a
16

torus.·
·_ _ _ _ /o/o/o/o ·
XX
·
00000•
2222222222 ·
· •
2222222222 ·
·
•
00000
·
·XX
·o/ o/ o/ o/ ·_ _ _ _
Each black and white pair are joined by a single edge, so G = K3,3, thecomplete bipartite graph with 3 black and 3 white vertices.
Describe B algebraically: use the orientation of X to define two permu-tations x and y of the set E of edges. For each e ∈ E, ex and ey are the nextedges around the incident black and white vertices, following the orientationof X. Warning: these are not generally automorphisms.
Black vertices oo // cycles of x on E
White vertices oo // cycles of y on E
Faces oo // cycles of xy on E
The orders l,m, n of x, y, xy are the least common multiples of their cyclelengths. Call (l,m, n) the type of B. E.g. B1 and B2 have type (3, 2, 2), B3
has type (3, 3, 3). The monodromy group of B is the subgroup G = 〈x, y〉generated by x and y in the symmetric group Sym(E) of all permutations ofE.G is connected, so G acts transitively on E, so the action is equivalent to
the action on the cosets Hg (g ∈ G) of a stabilizer H = Ge (e ∈ E). SayG acts regularly if Ge = 1; this action is equivalent to G acting on itself byright multiplication.
In B1, x3 = y2 = (xy)2 = 1, and these relations define the dihedral groupD3 of order 6, so G is a quotient of D3. G is transitive on the 6 edges, so|G : Ge| = 6 (the index of the subgroup), so G ∼= D3 with Ge = 1. G actsregularly. In B2, G ∼= D3, but |Ge| = 2, so the action is not regular.
17

In B3, G ∼= C3 × C3 acting regularly. Here x3 = y3 = 1 and xy = yx.
6.2 More Definitions
Algebraic bipartite map: (G, x, y, E) where G = 〈x, y〉 is a permutationgroup acting transitively on a set E. Reconstruct a bipartite map B from(G, x, y, E):
edges = elements of E
black/white vertices = cycles of x and y
faces = cycles of xy
Incidence = containment in a cycle.
Exercise 6.1 Take x = (1, 2, . . . , N) and y = (1, 2) in SN . Find B and G.
An automorphism of B is a permutation of E commuting with x and y,or equivalently commuting with G. E.g. rotations for the example dessins B1
and B3, translations for B3, but only the identity for B2. The automorphismsform a group
AutB = C(G) = C = c ∈ Sym(E) | cg = gc for all g ∈ G ,
the centraliser of G in Sym(E).A permutation group is semiregular (acts freely) if each stabiliser is triv-
ial.
The group is
semiregulartransitiveregular
as
at mostat leastexactly
one group elementtakes one point to another.
Thus regular ⇔ transitive and semiregular.
Theorem 6.1 Let G be any transitive group, and C = C(G) its centraliser.
(i) C acts semiregularly.
(ii) C acts regularly iff G does.
(iii) If C and G act regularly then C ∼= G.
Proof.
(i) Let c ∈ C fix e. Any e′ has the form e′ = eg for some g ∈ G bytransitivity. Then e′c = egc = ecg = eg = e′, so c = 1.
18

(ii) Let C act regularly. Then C is transitive, so its centraliser is semireg-ular by (i) applied to C; but G commutes with C, so G is semiregular,and being transitive it must be regular.
Conversely, let G act regularly, so it is acting on itself by right-multiplicationρg : e 7→ eg; then left-multiplication λc : e 7→ c−1e commutes withright-multiplication (c−1(eg) = (c−1e)g), and acts transitively, so C istransitive, and C is semiregular by (i), so C is regular.
(iii) When C and G act regularly, then λg ↔ ρg gives the isomorphismC ∼= G.
A dessin B is regular if G (equivalently AutB) is regular in E. From thelast examples B1 and B3 are regular, B2 is not.
Exercise 6.2 Show that C ∼= NG(Ge)/Ge where NG(Ge) is the normaliserof Ge in G.
Exercise 6.3 If B is a regular dessin of type (l,m, n) with N edges, what isits genus? Are there finitely or infinitely many dessins of a given type andgenus?
19

Lecture 5by Prof. Jürgen Wolfart
7 Uniformisation and Fuchsian GroupsExercise 7.1 How does the dessin change if the Belyi function β is replacedby 1 − β, 1
β? How are the pole orders encoded in the dessin? Start by some
dessin, how can you modify β such that every edge • is replaced by• • ?
7.1 Uniformisation
Theorem 7.1 Let X be a connected manifold. There is always a ”universalsimply connected covering” F : Y → X, where Y is a simply connectedmanifold with the following uniqueness property. Let F ′ be any other coveringY ′ → X and p ∈ X, q ∈ Y , q′ ∈ Y ′ s.t. F (q) = p = F ′(q′) then there is aunique covering map f : Y → Y ′, such that f(q) = q′ making the diagram
Y
F @@@@@@@@f //_______ Y ′
F ′~~
X
commute i.e. F = F ′ f .
”Covering” means: ∀p ∈ X∃U = U(p) s.t. F−1U =⋃
Vn (disjoint union)where F |Vn : Vn → U is a homeomorphism.
Proposition 7.2 X is a Riemann surface⇒ Y is simply connected Riemannsurface, F holomorphic and unramified.
Contruction of Y and F is given by homotopy theory. As a set,
Y = (p, [γ]) | p ∈ X, [γ] ∈ π1(X, p)
(closed curves modulo homotopy, with starting point p). Define a topology,define F as projection, control properties, in particular simple connectedness.
Theorem 7.3 (Extended Riemann Mapping Theorem, Main Theo-rem of Uniformisation) If Y is simply connected, Y is isomorphic to C,C or to H ∼= D (open unit disc).
20

Theorem 7.4 Every Riemann surface X is homeomorphic to some quotientspace G\Y where Y is the universal covering space and G is the ”coveringgroup” ⊂ Aut Y consisting of all γ ∈ Aut Y with F γ = F permutingtransitively the fibers of F .
(⇐ uniqueness part of theorem 7.1.) G acts without fixed points, it istorsion free, it acts discontinuously.
Here ”discontinuously” (properly) means: ∀q ∈ Y ∃V = V (q) s.t. V ∩γV = ∅ except for finitely many γ ∈ G.
Proposition 7.5 a) Y = C, Aut C ∼= PSL2(C)
X = C⇐ G = id ⇐
z 7→ az+bcz+a
have fixed points
b) Y = C, Aut C = z 7→ az + b | a ∈ C∗, b ∈ C
G ⊂ translations ⇐ no fixed point iff a = 1
It follows that G either ∼= Z or a lattice Λ. Also X = C or Z\C orΛ\C, a torus (elliptic curve). For example in the case X = Z\C
F (z) = exp z, F : C→ C∗ = C− 0
and exp(z + 2πik) = exp(z) for all k ∈ Z.
c) Y = H ∼= D in all other cases, in particular for all compact Riemannsurfaces X with g > 1. Here G ⊂ Aut H and it is called ”Fuchsiangroup”.
In general, discontinuous groups may have fixed points, i.e. points p ∈ Ywith a finite
Gp := γ ∈ G | γ(p) = p 6= id .
Theorem 7.6 For a discontinuous group G acting on Y = C, C, H the fol-lowing holds:
a) for p ∈ G, γ(p) = p there exists a local chart such that diagram
U(p)_
z
γ // U(p)_
z
D
z 7→ζknz// D
commutes and z 7→ zn : D → D induces the quotient map U → Gp\Ufor Gp = 〈γ〉.
21

b) all stabilizing subgroups are finite cyclic
c) fixed points of G form a discrete subset
d) G\Y has a holomorphic structure as a Riemann surface s.t. the quo-tient map Y → G\Y : z 7→ Gz is holomorphic, ramified of multiplicityn in fixed points of order n.
For now Y = H and G discontinuous ⊂ Aut H.
Theorem 7.7 Aut H = PSL2(R), the group of orientation preserving hyper-bolic motions.
It is clear that Aut H ⊇ PSL2 R, acting (simply) transitively on pointsand lines, by conjugation with a Cayley map pass to γ ∈ Aut H by com-bination with some µ ∈ PSL2 R, suppose γ(i) = i, suppose γ ∈ Aut D, andγ(0) = 0. Lemma (Schwarz): If holomorphic δ : D→ D has δ(0) = 0, then
|δ(z)| ≤ |z| ∀z ∈ D with ”=” iff
δ(z) = λz with |λ| = 1.
Hence, δ and its inverse mapping satisfy both |δ±1(z)| ≤ |z|, therefore δ(z) =λz is a hyperbolic motion ⇒ .
Theorem 7.8 G ⊂ PSL2(R) acts discontinuously on H, iff G is a discretesubgroup of PSL2(R).
7.2 Fuchsian Groups
There are two methods for the contruction of Fuchsian groups:
• Arithmetic: Construct discrete groups of PSL2 R by number theory,e.g. Γ = PSL2 Z (modular group).
• Geometry (Poincaré): Start with a ”suitable” hyperbolic polygon F(later serving as the fundamental domain for G), and generate G byside-pairing transformations.
Example: the ”triangle groups” 〈l,m, n〉 (drawing in D instead of H),l,m, n ∈ N\0 or ∞ with
1
l+
1
m+
1
n< 1.
22

πl
F
πm
πn
For example 〈2, 3,∞〉 = PSL2 Z and
〈∞,∞,∞〉 = Γ(2) = γ ∈ Γ = PSL2 Z | γ ≡ E mod 2
Also Γ/Γ(2) = PSL2(Z/2Z) ∼= S3. Fact: there are 85 triangle groups whichare ”arithmetically defined” (Takeuchi ∼ 1970).
γl0 = 1 = γm
1 = γn∞ = γ∞γ1γ0.
Theorem 7.9 a) These triangle groups 〈l,m, n〉 = 〈γ0, γ1, γ∞〉 are dis-continuous on H with F as ”fundamental region” (i.e. F open andF ∩ γF = ∅∀γ ∈ G− 1 and
⋃γ∈G γF = H) (hard work!)
...
d) There is a meromorphic G-invariant function j : H → C (j(γ(z)) =j(z)∀z ∈ H and γ ∈ G) mapping the two parts of F biholomorphicalyonto H and −H, border edges onto R and the vertices onto 0, 1,∞, withmultiplicities l,m, n.
Exercise 7.2 Let G be a (possibly ramified) covering group of X actingdiscontinuously on Y with X ∼= G\Y and let N C G normal subgroup,X ′ := N\Y . Show that G/N acts as group of automorphisms on X ′ s.t.
(G/N)\X ′ ∼= X.
Give an example of a Riemann surface with an automorphism group PSL2(Z/NZ),N ∈ N\0.
23

Lecture 6by Prof. Gareth Jones
8 Continued from Lecture 4
8.1 More on Dessins
Isomorphism of dessins: If B = (G, x, y, E) and B′ = (G′, x′, y′, E ′) are bi-partite maps (=dessins), then an isomorphism i : B → B′ consists of agroup-isomorphism θ : G → G′ sending x to x′, y to y′, and a bijectionφ : E → E ′ compatible with θ, i.e. φ(eg) = φ(e)θ(g) for all e ∈ E and for allg ∈ G:
E ×G
θ
φ
// E
φ
E ′ ×G′ // E ′
Theorem 8.1 Every dessin B is isomorphic to A\B for some regular dessinB and subgroup A ⊆ Aut B.
Proof. Take G to be the monodromy group of B, and take B to be the dessincorresponding to the regular representation of G, so B is regular (Theorem2.1). Take A = λg | g ∈ Ge for some e ∈ E; then orbits of A on E are justcosets Geg (g ∈ G), so A\B ∼= B.
Call B the canonical regular cover of B.
Exercise 8.1 Let B consist of a path of N edges, alternately white, black,white, etc. • • . . . Find G, C, B and A for thisdessin.
What about embeddings of graphs G which are not necessarily bipartite,e.g. the tetrahedron or octahedron?
Convert G into a bipartite graph by regarding the vertices of G as blackvertices, and placing a white vertex in each edge of G.
•
G
•
~~~~~~~
//
• •B=Gbip
~~~~~~~
24

This gives a bipartite graph Gbip. Any embedding of G in a surface gives abipartite map B. The edges of B correspond to the directed edges (=darts)of G. The rotations x and y of the set E of edges of B correspond to rotationsx and y of the set Ω of darts of G. So x rotates darts α around their incidentvertices following the orientation of the surface amd y reverses the directionof each dart, so y2 = 1.
We can define an algebraic map (not necessarily bipartite) to be a 4-tuple(G, x, y, Ω) where G = 〈x, y〉 is a transitive permutation group acting on Ω,with y2 = 1. As before, we can identify the vertices, edges and faces withcycles of x, y and xy on Ω, incidence given by non-empty intersection.
The algebraic theory is similar to that for bipartite maps.
8.2 Example
M, Monsieur Mathieu:
2 -- 1qq•OO3
4 • oo6 7
//OO5
8
•
•??9
12~~~~~~~ __ 10
11@@@@@@@
• •
Here |Ω| = 12. So
x = (1 2 3)(4 5 6)(7)(8 9 10)(11)(12)
andy = (1 2)(3 4)(5 8)(6 7)(9 12)(10 11).
Now G = 〈x, y〉. GAP ⇒ |G| = 95040, G ∼= M12.Finite simple groups (classified ∼ 1980): Cp, An, where (n ≥ 5), groups
of Lie type, e.g. PSL2(Fq), 26 sporadic groups, e.g. Mathieu group Mn wheren = 11, 12, 22, 23, 24. In this example, Gα
∼= M11 for α ∈ Ω. M has genus 0,and type (3, 2, 11). The corresponding bipartite map B has canonical regularcover B of type (3, 2, 11) and genus g = 3601 (see Exercise 2.3), Aut B ∼= M12.
By Belyi’s theorem B corresponds to an algebraic curve defined over analgebraic number field. The field of definition is Q(
√−11). This has Galois
25

group isomorphic to C2, generated by complex conjugation. Applying thisto the coefficients of the algebraic curve and the Belyi function, we get themirror image of M, M. Later we will see more interesting and less obviousactions of Galois groups of maps.
9 Galois Theory
9.1 Basic Galois Theory
Every field F has an algebraic closure F , a minimal extension field of F overwhich every f ∈ F [x] splits into linear factors. This field F is:
• unique up to isomorphisms fixing F ,
• an algebraic extension of F , i.e. every α ∈ F is a root of some non-zerof ∈ F [x], or equivalently |F (α) : F | <∞.
Important case:
Q := α ∈ C | f(α) = 0 for some non-zero f ∈ Q[x]
the field of algebraic numbers. Motivation: Belyi’s Theorem.A field extension K ⊇ F is normal (or Galois) if every embedding e :
K → F (fixing F ) satisfies e(K) = K.(Strictly speaking, ”Galois = normal and separable”, where ”separable”
means that irreducible polynomials don’t have repeated roots; all fields ofcharacteristic 0 are separable, so we’ll ignore this point by assuming thatchar F = 0 for all fields F mentioned.)
Example 9.1 F = Q, K = Q(ζn) the nth cyclotomic field, ζn = exp(2πin
).Any embedding e : K → Q sends ζn to some ζj
n ∈ K, so e(K) = K. This isa Galois extension.
Example 9.2 F = Q, K = Q(α), α = 21/3 ∈ R. There is an embeddinge : K → Q sending α to αζ3 /∈ K. This extension is not Galois.
Theorem 9.1 K ⊇ F is a finite Galois extension if and only if K is thesplitting field of some f ∈ F [x].
The Galois group Gal K of a field K is the group of all field automor-phisms of K. If H ≤ Gal K, then fix H is the subfield fixed pointwise by H.If F ⊆ K then Gal K/F is the subgroup of Gal K fixing F pointwise.
In Theorem 9.1 G = Gal K/F permutes the roots of f faithfully so wecan embed G in Sn, n = deg(f) =”no. of roots of f ”, and |G| = |K : F |.
26

Example 9.3 K = Q(α, ζ3), α = 21/3 ∈ R as before, F = Q. K is the split-ting field of f(x) = x3− 2. Degree is |K : F | = 6, basis 1, α, α2, ζ3, αζ3, α
2ζ3.f has three roots αj = αζj
3 (j = 0, 1, 2) permuted faithfully by G = Gal K/F ,so G → S3. Since |G| = |K : F | = 6 and |S3| = 6, G ∼= S3.
Theorem 9.2 (Fundamental Theorem of Galois Theory) Let K ⊇ Fbe a finite Galois extension, G = Gal K/F . There is an order-reversingbijection L 7→ H = Gal K/L between fields L such that K ⊇ L ⊇ F , andsubgroups H ≤ G. The inverse sends each H to L = fix H. We have |K :L| = |H| and |L : F | = |G : H|. L ⊇ F is Galois iff H E G, in which caseGal L/F ∼= G/H.
KXX
00
00
00
00 G
L oo // H
F
FF
1
In example 1,
Gal Q(ζn)/Q = θj : ζn 7→ ζjn | (j, n) = 1 ∼= Un = Z∗
n,
the group of units mod n. This is abelian, so all subfields of Q(ζn) areGalois over Q.
In example 3, S3 B A3∼= C3, and the field L corresponding to H = A3
is the Galois extension Q(ζ3) of Q. The subfield L = Q(α) corresponds to anon-normal subgroup of G
Exercise 9.1 Find the splitting field K of xn− 2, describe the Galois groupof K, and find the subgroups fixing 21/n ∈ R and ζn.
9.2 The Absolute Galois Group
The absolute Galois group of a field F is Gal F /F . The absolute Galois groupis Gal Q/Q, denoted by G. Let K denote the set of all finite Galois extensionsK of Q, and let GK = Gal K/Q, a finite group of order |K : Q|.
Theorem 9.3 (i) Q is the union of all the fields K ∈ K
(ii) Each K ∈ K is invariant under G.
Proof.
27

(i) Each K ∈ K is a finite extension of Q, so if α ∈ K then |Q(α) : Q| ≤|K : Q| < ∞, so α ∈ Q. Conversely, if α ∈ Q then f(α) = 0 for somenon-zero f ∈ Q[x], and α ∈ K =”splitting field of f ”.
(ii) Follows by definition of ”Galois”.
Thus each g ∈ G is uniquely determined by its restrictions gK ∈ GK tothe fields K ∈ K. If K ⊇ L where K, L ∈ K then L is invariant under GK sothere is a restriction homomorphism ρK,L : GK → GL sending gK to gL, i.e.
ρK,L(gK) = gL
whenever K ⊇ L. Conversely if we have elements gK ∈ GK for each K ∈ K,with ρK,L(gK) = gL whenever K ⊇ L, we can define g ∈ G by g(α) = gK(α)where α ∈ K ∈ K. (Check independence of K.) We can therefore identifyG = Gal Q with the group
(gK) ∈ Π := ΠK∈KGK | ρK,L(gK) = gL whenever K ⊇ L in K,
the subgroup of the cartesian product Π consisting of elements whose coor-dinates are compatible with the ρK,L’s.
This is the projective limit lim←−GK of the finite groups GK and homomor-phisms ρK,L, a profinite group.
Exercise 9.2 Show that⋃
n≥1 Q(ζn) is a subfield of Q, and describe its Ga-lois group.
Exercise 9.3 What are the cardinalities of Q and G?
To get a bijection between fields and groups, we need some topology:Put the discrete topology on each GK (K ∈ K), so all subsets are open
and closed. This induces a product topology on Π, the weakest such that theprojections Π→ GK are continuous. G → Π, so G inherits a topology fromΠ, the Krull topology. (Intuitively, elements of G are ”close together” if theyagree on a large subfield of Q.) Multiplication and inversion are continuousin each GK , and hence also in Π and G, so these are topological groups.
Exercise 9.4 Show that G is a closed subgroup of Π, and both Π and G arecompact Hausdorff spaces.
Warning: G is topologically unpleasant: homeomorphic to a Cantor set.The Fundamental Theorem (9.1) extends to the extension Q ⊇ Q pro-
vided we restrict the bijection to the closed subgroups of G, not all subgroups.
28

Exercise 9.5 In any topological group, every open subgroup is closed, andevery closed subgroup of finite index is open.
29

Lecture 7by Prof. Jürgen Wolfart
10 Continued from Lecture 5Theorem 10.1 a) Fuchsian triangle groups G are discontinuous on H
with F as ”fundamental domain”.
b) G is generated by γ0, γ1, γ∞ (by any two of them)
c) G is presented by 〈γ0, γ1, γ∞ | γl0 = γm
1 = γn∞ = 1 = γ∞γ1γ0 〉
d) There is a meromorphic G-invariant (G-”automorphic”) function j :H → C mapping the two (open) parts of F onto H and −H, borderedges on R, vertices to 0, 1,∞ with ramification multiplicities l,m, n.
e) j provides an identification of G\H with C (in case that l,m, n finite)
Remark : In case of cusps, omit these points! I.e. for G = 〈∞,∞,∞〉 ∼=Γ(2), j : H→ C− 0, 1,∞ universal covering map!
Exercise 10.1 Show that 〈 2, 2, n 〉 = G is a ”spherical” trianglegroup and
j(z) =1
4
(2 + zn +
1
zn
).
10.1 Remarks
Triangle groups are (the only) ”rigid” Fuchsian groups, i.e. uniquely deter-mined by their presentation up to conjugation in PSL2(R).
There is a bijection between G − automorphic functions on H andmeromorphic functions on G\H .
10.2 More General Facts about Fuchsian Groups
Theorem 10.2 a) Let p ∈ H be a non-fixed point for G and let d be thehyperbolic distance on H. Then (Dirichlet)
F := z ∈ H | d(p, z) < d(γ(p), z) ∀γ ∈ G − id 6= ∅
is a fundamental domain for G bounded by side-edges
lσ := z ∈ H | d(p, z) = d(σ(p), z), σ ∈ G − idd(p, z) ≤ d(z, γ(z)) ∀γ ∈ G − id, σ .
30

b) For all compact C ⊂ H, lσ ∩ C 6= ∅ for finitely many σ ∈ G only. Fcompact ⇒ F is a finite convex polygon bounded by finitely many sideedges, F compact ⊂ H ⇔ X = G\H is a compact Riemann surface.
c) G is generated (finitely in the ”cocompact” case) by ”side-pairing” trans-formations σ ∈ G sending lσ−1 to lσ, sending F to a neighbour σF withcommon side lσ.
d) Loops around vertices of F relations between these generators presentation of G.
e) (Poincaré) If F is an H-polygon with side-pairings and some conditionon the angles guaranteeing that locally around F , the images γF haveno overlapping ⇒ the plane is covered by GF without overlappings andwith H = GF , G = 〈 side-pairings 〉.
Example (in D): Let F be an 8-sided polygon with side-pairings as indi-cated below,
•
••
••
••
••
••
••
••
•
........................ . . . . . . . . . ...
..==
. ................SS
.................
. . . . . . . .. .
. ....................
.....
....................~~
δ
γα
β
∑all angles = 2π ⇒
G = 〈α, β, γ, δ |αβα−1β−1γδγ−1δ−1 = 1 〉
is a Fuchsian group with G\H = X compact of g = 2. This G is not rigid!G\H has six real free parametres ⇒ ”Teichmüller space”.
31

Theorem 10.3 a) Suppose G ⊂ ∆ are Fuchsian, (∆ : G) <∞ with ∆ =⋃·k Gγk, ∆ has F∆ as a fundamental domain. Then FG :=
⋃k γkF∆ is
a fundamental domain for G (⇒ inducing a triangulation of X = G\Hif ∆ is a triangle group).
b) Let X, X ′ be Riemann surfaces with surface (universal covering) groupsG,G ′ ⊂ Aut H = PSL2 R. Then X ∼= X ′ iff G and G ′ are conjugate inPSL2 R.
H
γ∈Aut H// H
X
∼= // X ′
(γ well defined ⇔ induces a conjugation G → G ′)
Recall that X compact Riemann surface is a smooth projective algebraiccurve given by some equations. In case g > 1, X = G\H with some Fuchsiangroup G. How are the equations determined by G and conversely?
Theorem 10.4 Suppose X is a (compact) projective smooth algebraic curve.It has a Belyi function β : X → C (i.e. can be defined over Q) ⇔ there is atriangle group ∆ = 〈 l,m, n 〉 (cocompact) and a finite index subgroup G ⊆ ∆s.t. X ∼= G\H
Proof.
”⇐”: If X ∼= G\H, G ⊆ ∆, then j : H → C with the j-function for ∆ =〈 l,m, n 〉 induces a well-defined meromorphic mapping β : Gz 7→ j(z)ramified only in points G∆p0,G∆p1,G∆p∞ ∈ X = G\H (pi fixed underγi), therefore a Belyi function; the dessin given by the ∆-tesselation onthe upper half-plane H, take the quotient by G.
”⇒”: Start with a Belyi function β : X → C s.t. least common multiple (lcm)of all multiplicities above 0, (1,∞) is l, (m,n). (Any common multipledoes as well!) ∆ = 〈 l,m, n 〉 ⊂ PSL2 R and its j-function ⇒ β−1 isonly locally biholomorphic outside 0, 1,∞, but β−1 j is everywherelocally well-defined, holomorphically, so
w_
Hh
j
@@@@@@@@ w
AAAAAAAA
wl/l′
CCCCCCCCC
CCCCCCCCC Xβ // C wl
z // zl′
32

commutes. H simply connected, so (by the monodromy theorem) β−1jcan be defined globally as holomorphic map h
h(z) = h(z′)⇒ z ∈ ∆z′
So X ∼= G\H, where G is defined as γ ∈ ∆ |h(z) = h(γz) for all z ∈H .
10.3 Remarks
• In general, G is not the (unique) surface group for X, because it canhave torsion. But if l′ = l etc., i.e. if β has the same multiplicity l (m,n) in all zeros (1-points, poles), then h is the universal covering map,G is the surface group of X. This occurs precisely, if the dessin for βis ”uniform” (⇐ regular dessins).
• deg β = (∆ : G).
33

Lecture 8by Prof. Gareth Jones
11 From Dessins to Holomorphic Structures
11.1 Coverings
Let B = (G, x, y, E) and B′ = (G′, x′, y′, E ′) be algebraic bipartite maps.A morphism γ : B → B′ or covering consists of a group-homomorphismθ : G → G′ and a function φ : E → E ′ such that x 7→ x′ and y 7→ y′ underθ, and φ(eg) = φ(e)θ(g) for all e ∈ E, and for g = x, y (equivalently for allg ∈ G).
Example: B1 → B2 = C2\B1 in section 6, lecture 4.More generally, B → A\B = B′, where A ≤ AutB with G′, x′, y′ the
actions of G, x and y on the orbits of A. Coverings induced by automorphismsin this way are regular, or normal.
Exercise 11.1 Show that θ and φ must be epimorphisms.
γ is an isomorphism iff θ and φ are bijections, and then an automorphismif B = B′.
Exercise 11.1AutB = C(G) ∼= NG(Ge)/Ge.
Algebraic bipartite maps form a category.The topological analogue of a morphism γ is a branched covering X → X ′
of surfaces, preserving orientation, with black vertices, white vertices, edgesand faces on X ′ lifting to the same on X, and branching only at vertices orface-centers. We have a category of topological bipartite maps, and lecture4 described a functor from these to algebraic bipartite maps. We can easilyreverse this process, but with more work we can obtain holomorphic, ratherthan topological structures from algebraic bipartite maps.
11.2 Triangle Groups and Bipartite Maps
Consider algebraic bipartite maps of a given type (l,m, n), so in G we havexl = ym = zn = xyz = 1. Consider the (abstract) group
∆ = ∆(l,m, n) = 〈X, Y, Z |X l = Y m = Zn = XY Z = 1 〉
34

G is a quotient of ∆ by X 7→ x, etc. Then ∆ → G → Sym(E) givesa transitive action of ∆ on the edge set E of B. Bipartite maps of type(l,m, n)↔ ”transitive actions of ∆”. (Warning: actions of ∆ can give mapsof type (l′, m′, n′) where l′|l, etc.) These actions correspond to conjugacyclasses of subgroups ∆e ≤ ∆ (e ∈ E). B is finite (compact)⇔ |∆ : ∆e| <∞.Coverings B → B′ correspond to inclusions ∆e ≤ ∆e′ (easy exercise). Regularcoverings correspond to normal inclusions. AutB ∼= N∆(∆e)/∆e (exercise2.2) Theorem 2.1 and exercise 2.2 give
Theorem 11.1 B is regular if and only if ∆e E∆, in which case
G ∼= AutB ∼= ∆/∆e.
Example 11.1 Let B correspond to the regular representation of G = Cn ×Cn = 〈x, y |xn = yn = 1, xy = yx 〉. Then xy has order n, so the typeis (n, n, n). Take ∆ = ∆(n, n, n), ∆e = Ker(∆ → G) E ∆. G is abelian,so ∆e ≥ ∆′ = ”commutator subgroup of ∆”. Both have index n2 in ∆, so∆e = ∆′. Here G ∼= AutB ∼= ∆/∆e = ∆ab.
The triangle group of type (l,m, n) has the same presentation as ∆ (gener-ators γ0, γ1, γ∞ in Jürgen’s lectures), so identify ∆ with this group, X, Y, Z =”rotations through 2π
l,2π
m,2π
nabout the vertices of a triangle T with internal
angles πl, πm
,πn”. Assume that 1
l+ 1
m+ 1
n< 1 (typical case); if not, replace H
with C or C. H is tesselated by the images of T under the extended trianglegroup ∆[l,m, n] generated by reflections in the sides of T , and ∆ = ∆(l,m, n)is the even subgroup of index 2, preserving orientation.
We can colour the vertices black, white or red as they are images of thevertices of T fixed by X, Y or Z. Every triangle has one vertex of eachcolour. Their valencies are 2l, 2m, 2n respectively.
••
••
••
••
A\A_A
@@@@@@@@@@@@ D
••
••
••
••
Delete red vertices (∗)and incident edges
//
This gives a bipartite map of type (l,m, n) on H. This is the univer-sal bipartite map B∞(l,m, n) of type (l,m, n). It is a regular map, withAutB∞(l,m, n) = ∆(l,m, n), edge-stabiliser ∆e = 1.
35

Theorem 11.2 Every bipartite map B of type (l,m, n) is isomorphic to aquotient A\B∞(l,m, n) of B∞(l,m, n) by a subgroup A ≤ AutB∞(l,m, n).
Proof. Take A to consist of the automorphisms of B∞(l,m, n) induced bythe subgroup ∆e of ∆, and check that B ∼= A\B∞(l,m, n).
11.3 Holomorphic Structures
A\B∞(l,m, n) has extra holomorphic structure, so denote it by Bhol. H isa Riemann surface, and ∆e acts as a discontinuous group of automorphismsof H (since ∆ does), so Bhol is on a Riemann surface X = A\H. CoveringsB → B′ of bipartite maps correspond to inclusions ∆e ≤ ∆e′ in ∆, so theseinduce branched coverings X → X ′ of Riemann surfaces. In particular, if wetake ∆e′ = ∆, so |E ′| = 1 corresponding to the trivial bipartite map withone edge, we get a covering X → X ′ = C branched only over the vertices0 and 1, and the face-centre at ∞. This is a Belyi function (provided X iscompact, i.e. B is finite). Then Belyi’s Theorem gives:
Theorem 11.3 If B is a finite algebraic map, then the Riemann surface Xunderlying Bhol is defined, as a smooth projective algebraic curve, over thefield Q of algebraic numbers.
Example 11.2 (Example 4.1 revisited) If B is as in example 11.1, theRiemann surface X uniformised by ∆′ (=”commutator subgroup of ∆ =∆(n, n, n)”) is the nth degree Fermat curve F = Fn with affine equationxn + yn = 1, with Belyi function β : (x, y) 7→ xn. The black vertices areat (0, ζj
n) j = 0, 1, . . . , n − 1, and the white vertices are at (ζkn, 0) k =
0, 1, . . . , n − 1. The edges (given by β−1([0, 1])) between vj = (0, ζjn) and
wk = (ζkn, 0) are given by (rζk
n, sζjn) where r, s ∈ [0, 1] and rn + sn = 1.
In general,
AutB ∼= AutBhol ∼= N∆(∆e)/∆e
≤ NPSL2 R(∆e)/∆e (since ∆ ≤ PSL2 R)∼= Aut X.
Thus automorphisms of B act as automorphisms of the Riemann surface X(equivalently, of the algebraic curve).
Example 11.3 (=Examples 1 and 2 revisited) If B is as in Example11.1 and 11.2, then AutB ∼= Cn × Cn, and this acts on X by multiplying x
36

and y independently by nth roots of 1. In this case, AutB 6= Aut X, sinceAut X is a semidirect product (Cn × Cn) o S3 of AutB by a complementS3. The extra S3 comes from permuting the 3 vertex-colours, or alternativelywrite X in projective form as xn + yn + zn = 0, and let S3 permute thecoordinates.
Exercise 11.2 Explain example 11.3 by describing NPSL2 R(∆e).
11.4 Non-cocompact Triangle Groups
Suppose we want to consider all bipartite maps B of type (3, 2, n) withoutrestricting n. We take
∆ = ∆(3, 2,∞) = 〈X, Y, Z |X3 = Y 2 = Z∞ = XY Z = 1 〉= 〈X, Y |X3 = Y 2 = 1 〉 eliminating Z = (XY )−1
∼= C3 ∗ C2.
The algebraic theory works as before. Geometrically, we take T to have ablack vertex at i (angle π
2) and white vertex at ζ3 (angle π
3), and a red vertex
at∞ on ∂H (angle π∞ = 0). Reflections in the sides of T generate ∆[3, 2,∞],
the images of T tesselate H, with vertices at the images of ∞.
Exercise 11.3 Show that ∆[3, 2,∞] = PGL2(Z), consisting of the transfor-mations
τ 7→ aτ + b
cτ + da, . . . , d ∈ Z, ad− bc = 1
orτ 7→ aτ + b
cτ + da, . . . , d ∈ Z, ad− bc = −1.
The first type form the even subgroup Γ = PSL2(Z).
The orbit of ∞ under Γ is P1(Q) = Q ∪ ∞, so this is the set of redvertices. Deleting the red vertices and their incident edges, we get a bipartitemap B∞(3, 2,∞) of type (3, 2,∞). If ∆e is a subgroup of finite index in∆ = Γ, then ∆e\H is a compact Riemann surface minus finitely many points,one for each orbit of ∆e on P1(Q)
To deal with bipartite maps B of all possible types, use ∆(∞,∞,∞) =Γ(2), congruence subgroup of level 2 in Γ. Here T has 3 vertices on ∂H, at0, 1 and∞. Γ(2) is the even subgroup of ∆[∞,∞,∞] = ”group generated byreflections in the sides of T ”. Images of T tesselate H, vertices are elementspq∈ P1(Q), coloured black, white, red, as p is even and q is odd, or p and q are
both odd, or p is odd and q is even (orbits of Γ(2), see Exercise 2.3). Deleting
37

red vertices and incident edges gives B∞(∞,∞,∞) = B∞, the universalbipartite map. Every B is a quotient of B∞.
Exercise 11.4 Draw B∞!
38

Lecture 9by Prof. Gareth Jones
12 Quasiplatonic Surfaces, and Automorphisms
12.1 Definitions and Properties
Any compact Riemann surface X of genus g > 1 can be uniformised byan essentially unique (upto conjugation by isometries) torsion-free Fuchsiangroup K (∼= π1X). Isomorphisms X → X ′ are induced by conjugatingisometries of H taking K to K ′. Taking X = X ′ we see that automorphismsof X are induced by isometries normalising K. Since K acts trivially onK\H, we get
Aut X ∼= N(K)/K
where N denotes the normalizer in PSL2 R. (If g = 1, replace H with C,replace K with a lattice Λ unique up to similarity — see the Elliptic Curveslecture.) We say that X (compact, of genus g > 1), is quasiplatonic if Xis uniformised by a subgroup K as above, with K normally contained in atriangle group.
Theorem 12.1 If X is a compact Riemann surface of genus g > 1, thefollowing are equivalent:
a) X is quasiplatonic,
b) N(K) is a triangle group (K as above)
c) X has a Belyi function β : X → C which is a regular covering,
d) X corresponds to a regular dessin.
Proof.
a) ⇒ b): N(K) is a Fuchsian group (since K is) and it contains a triangle group.Any Fuchsian group containing a triangle group must be a trianglegroup (by Teichmüller theory — triangle groups are the only rigid Fuch-sian groups).
b) ⇒ c): Inclusion K ≤ N(K) induces a Belyi function
X ∼= K\H→ N(K)\H ∼= C.
Since K EN(K), this is a regular covering.
39

c) ⇒ d): Use β to lift the trivial dessin ( 0 1
• ) on C to X, and since β isregular we get a regular dessin on X.
d) ⇒ a): If X corresponds to a regular dessin B, then K is normal in the corre-sponding triangle group.
Example 12.1 The nth degree Fermat curve (n > 3) corresponds to a regulardessin, and is uniformised by the commutator subgroup of ∆(n, n, n) whichis normal.
Exercise 12.1 For genus g = 1, what are the analogues of the quasiplatonicsurfaces?
One can characterise the quasiplatonic surfaces as the local maxima for|Aut X|, in the sense that, within the Teichmüller space of all compact Rie-mann surfaces of genus g, every other surface sufficiently close to X has fewerautomorphisms.
12.2 Hurwitz Groups and Surfaces
Here we look for global maxima of |Aut X|.Problem: Given g > 1, what are the most symmetric Riemann surfaces
of genus g?We have Aut X ∼= N(K)/K, with N(K) Fuchsian. The index |N(K) : K|
is finite, equal to the ratio of the areas of the fundamental regions of thesetwo groups. For K this is 4π(g − 1), so maximising |Aut X| is equivalentto minimising the area for N(K). One can show that among all Fuchsiangroups, this area is minimised by the triangle group ∆(3, 2, 7) = ∆(2, 3, 7),given by
∆ = 〈X, Y, Z |X3 = Y 2 = Z7 = XY Z = 1 〉.
Exercise 12.2 Prove that ∆ has a fundamental region of area π21
, and thisis the minimum among all triangle groups. Use the Gauss-Bonnet formula:”area”=π − α− β − γ for a hyperbolic triangle with internal angles α, β, γ.
This gives us the Hurwitz bound
|Aut X| ≤ 4π(g − 1)
π/21= 84(g − 1),
40

attained iff X ∼= K\H where K is a normal subgroup of finite index in∆ = ∆(3, 2, 7). (Every proper normal subgroup in ∆ is torsion-free, easyexercise.) These surfaces X and finite groups G = Aut X are called Hurwitzsurfaces and Hurwitz groups. These surfaces are all quasiplatonic.
Example 12.2 The modular group Γ = PSL2(Z) = ∆(3, 2,∞) maps ontoG = PSL2(7) = PSL2(Z7) by reducing coefficients mod 7. The generatorZ : τ 7→ τ + 1 is mapped to an element z of order 7 in G, so G is a quotient∆/K of ∆ = ∆(3, 2, 7).
|G| = 168
(=
7(72 − 1)
2
),
so the surface X = K\H has genus g = 1 + 16884
= 3. This is Klein’s quarticcurve, given in projective coordinates by
x3y + y3z + z3x = 0,
with Aut X ∼= PSL2(7).
Exercise 12.3 Prove that there is no Hurwitz group of genus 2.
12.3 Kernels and Epimorphisms
It’s useful to count normal subgroups K of a triangle group ∆ with a givenquotient group G ∼= ∆/K.
Proposition 12.2 If ∆ is any finitely generated group, and G is any finitegroup, the number n∆(G) of K E∆ with ∆/K ∼= G is given by
n∆(G) =|Epi(∆, G)
|Aut G|,
where Epi(∆, G) is the set of all epimorphisms θ : ∆→ G.
Proof. These normal subgroups K are the kernels of the epimorphismsθ : ∆ → G, and ker θ = ker θ′ iff θ′ = α θ for some α ∈ Aut G. Hence thekernels correspond to the orbits of Aut G acting by composition on Epi(∆, G).
∆θ′
!!CCCCCCCCθ
G α// G
41

Since Aut G acts semiregularly (i.e. α θ = θ ⇒ α = id), its orbits all havesize |Aut G|. By the hypotheses, Epi(∆, G) is finite, so the result follows.
For many G, |Aut G| is known or easily found, so concentrate on countingepimorphisms. If ∆ is a triangle group
∆(l,m, n) = 〈X,Y, Z |X l = Y m = Zn = XY Z = 1 〉,
finding epimorphisms ∆→ G is equivalent to finding triples x, y, z ∈ G suchthat
a)xl = ym = zn = xyz = 1
(so there is a homomorphism ∆→ G : X 7→ x etc.)
b) G is generated by x, y and z (or by any two of these), so we have anepimorphism.
If we want K to be torsion-free, we also require:
c) x, y and z must have orders exactly l,m and n.
12.4 Direct Counting
Example 12.3 Let ∆ = ∆(5, 2,∞) and G = A5, so we count K E ∆ with∆/K ∼= A5. This is equivalent to counting regular maps M (m = 2) withvalency 5 (l = 5) and AutM ∼= A5. A5 has 24 elements x of order 5 (the5-cycles), and 15 elements of order 2 (the double transpositions (ab)(cd))giving 24 × 15 = 360 pairs x, y satisfying the relations of ∆. The subgroupH = 〈x, y 〉 has order divisible by 10, so H ∼= D5 or H = A5. Thereare 6 subgroups H ∼= D5, each generated by 4 × 5 = 20 pairs x, y, so 120pairs don’t generate A5. Hence 360 − 120 = 240 do generate A5. Thus|Epi(∆, G)| = 240. Now Aut A5 = S5 (acting by conjugation) of order 120,so n∆(G) = 240
120= 2. Thus ∆ has two normal subgroups K with ∆/K ∼= A5,
i.e. there are two regular 5-valent maps M with AutM ∼= A5. One is theicosahedron, represented by
θ : X 7→ x = (1, 2, 3, 4, 5), Y 7→ y = (1, 2)(3, 4), Z 7→ z = (2, 5, 4).
The other one is the great dodecahedron, with 12 pentagonal faces, and thevertices and edges of an icosahedron. It’s represented by
θ : X 7→ x = (1, 2, 3, 4, 5), Y 7→ y = (1, 3)(2, 4), Z 7→ z = (1, 2, 3, 5, 4).
42

This has genus g = 1 + N2(1 − 1
l− 1
m− 1
n) = 4 (where in this case N = 60
and l = 5, m = 2, n = 3.) The underlying algebraic curve is Bring’s curve,given in P4(C) by
xk1 + xk
2 + xk3 + xk
4 + xk5 = 0 (k = 1, 2, 3).
Aut X ∼= S5 (permuting the coordinates), and the subgroup A5 is the auto-morphism group of the map.
12.5 Counting by Character Theory
A (complex) representation of a group G is a homomorphism ρ : G→ GL(V ),V a vector space over C. ρ : G→ GL(V ) and ρ′ : G→ GL(V ′) are equivalentif some isomorphism V → V ′ commutes with G. The representation ρ isirreducible is V has no G-invariant subgroups other than 0 and V . A finitegroup G has c irreducible representations, up to isomorphism, where c is thenumber of conjugacy classes in G. The character table of G is a c× c array,”entries” = ”trace of ρ(g) on each conjugacy class” (constant on each class).
Proposition 12.3 If X ,Y and Z are conjugacy classes in a finite group G,then the number of solutions of xyz = 1 in G with x ∈ X , y ∈ Y, z ∈ Z isequal to
|X | · |Y| · |Z||G|
·∑
χ
χ(x)χ(y)χ(z)
χ(1),
where χ ranges over the irreducible characters of G.
In A5 there are c = 5 conjugacy classes: the identity, 15 double transposi-tions, 20 3-cycles, and two classes of 12 5-cycles. Hence there are 5 irreduciblecharacters and the character table looks like in table 1 where λ, µ = 1±
√5
2.
1 (..)(..) (...) (.....)+ (.....)−
1 1 1 1 13 1 0 λ µ3 1 0 µ λ4 0 1 -1 -15 1 -1 0 0
Table 1: The character table of A5.
43

Example 12.4 Take ∆ = ∆(3, 3, 5), G = A5 and count KE∆ with ∆/K ∼=A5. There is only one choice for the classes X and Y of elements x, y oforder 3, and there are two choices for the class Z containing z of order 5.In each case there are 60 triples x, y, z in these classes satisfying xyz = 1,giving 120 triples. Hence there is 120
120= 1 normal subgroup K. This gives
a single regular bipartite map of type (3, 3, 5) with AutB ∼= A5. Exercise ⇒genus g = 5. It’s a double covering of the dodecahedron branched over the 12face-centres, with vertices coloured alternately black and white.
44

Lecture 10by Prof. Jürgen Wolfart
13 Moduli Fields and Fields of Definition”Existence of Belyi function β ⇒ X is defined over Q.”
K is a field of definition for the compact Riemann surface X iff X is iso-morphic to a smooth projective algebraic curve ⊂ PN(C) given by equationspi(x0, . . . , xN) = 0, all pi ∈ K[x0, . . . , xN ]. If K is a field of definition, thenC ⊃ L ⊃ K is a field of definition. Is there a minimal field of definition? Isit in Q?
LetGC := group of field automorphisms of C.
Suppose X to be defined over K by equations pi(x0, . . . , xN) = 0, take σ ∈GC, let Xσ be defined by the equations pσ
i (x0, . . . , xN) = 0 (apply σ to allcoefficients of all pi) ⇔
[σ(x0), . . . , σ(xN)] | [x0, . . . , xN ] ∈ X =: Xσ.
This is again a smooth curve!By the same reason
X
β
///o/o/o/o Xσ
βσ
C∼= // P1(C)
commutes. Here βσ is defined by applying σ to the coefficients of β, and itremains a Belyi function on Xσ, because vanishing of derivatives is preservedunder σ, and σ(0) = 0, σ(1) = 1, σ(∞) =∞. The list of all multiplicities ofβ is preserved under σ and degree of β equals to degree of βσ. This impliesthat σ maps the dessin D for β a dessin Dσ of the same type for βσ on Xσ.Now GC acts on dessins of a given type and with a given no. of edges! Finiteorbits ⇒
Theorem 13.1 a) The subgroup G(D) := σ ∈ GC |D∼= Dσ is of finite
index in GC.
45

b) σ ∈ G(D) ⇔ there exist (biholomorphic!) isomorphisms fσ : X → Xσ
for which
X
β
fσ // Xσ
βσ~~||||||||
Ccommutes with the respective Belyi functions.
c) The ”moduli field” M(D) := ζ ∈ C |σ(ζ) = ζ ∀σ ∈ G(D) has finitedegree [M(D) : Q] ⇒ is a numberfield. (Reason: all ζ ∈ M(D) havea finite orbit under GC, length of orbit is bounded by (GC : G(D)) ⇒[M(D) : Q] ≤ (GC : G(D)).)
Consequence: Also G(X) := σ ∈ GC | ∃ isomorph. fσ : X → Xσ andit follows that the corresponding fixed field M(X) of G(X) in ⊆M(D), andtherefore we have again a number field.
Theorem 13.2 M(X) depends only on the isomorphism class of X and iscontained in any field of definition for X (analoguous for M(D) ⊂ field ofdefinitions for X and β).
Suppose X ∼= X ′, i.e. there is an isomorphism h : X → X ′ and supposethat σ ∈ G(X), i.e. there is an isomorphism fσ : X → Xσ. We have anisomorphism hσ : Xσ → X ′σ and we can contruct an isomorphism to makethe diagram
Xh //
fσ
X ′
Xσ hσ
// X ′σ
commute. hσfσh−1 gives the isomorphism we are looking for⇒ σ ∈ G(X ′)⇒
G(X) ∼= G(X ′)⇒ claim.
Theorem 13.3 M(X) is a field of definition for X if g(X) = 0 or 1.
Proof. g = 0⇔ X ∼= C ∼= P1(C), defined /Q.g(X) = 1⇔ X ∼= Λ\C, Λ = Z⊕Zτ (τ ∈ H). X defined /Q(g2(τ), g3(τ)) ⊇
Q(j(τ)), so we see that X can be defined even over Q(j(τ)). Xσ defined/Q(σ(g2(τ)), σ(g3(τ))), even over Q(σ(j(τ))), where σ ∈ GC. So X ∼= Xσ ⇔σ(j(τ)) = j(τ). M(X) is generated by j(τ) and Q(j(τ)) is a field of defini-tion.
46

But: in high genera there are counter examples, where X cannot be de-fined over M(X). (Earle 1969, Shimura, Dèbes/Emsalem, Fuertes/Gonzalez).
Example by Earle in g = 2, ζ = ζ3 = e2πi3
X : y2 = x(x− ζ)(x + ζ)(x− ζ2t)(x +ζ2
t)
defined over Q(ζ), and where t ∈ Q, t 6= 0, 1, t > 0.
1. X cannot by defined over Q. Note that point pairs (∞,∞), (0, 0),(ζ, 0), (−ζ, 0),(ζ2t, 0), (− ζ2
t, 0) are ”intrinsic”, also their image points in
P1(C) under (x, y) 7→ x, upto PSL2 C-transformations. If X can bedefined over Q, then there is an anticonformal automorphism of X,permuting the critical points on P1(C): doesn’t exist (by calculation ofcross-ratios)!
2. M(X) = Q = R ∩ Q(ζ), X ∼= X, i.e. there is a holomorphic isomor-phism X → X. There is an anticonformal mapping (x, y) 7→ (− 1
x, iy
x3 ),which is in fact an anticonformal automorphism (of order 4).
Theorem 13.4 If M(X) ∈ Q, then X can be defined over a number field.(Weil, J.W., B. Köck)
Idea: Any field of definition K for X is finitely generated over M(X)because for a model of X defined over K
σ|K = id⇒ X = Xσ.
Suppose for simplicity K = M(X)(ξ) where ξ is transcendential, then thereexists σ ∈ GC, σ|M(X) = idM(X), σ(ξ) 7→ η (η any other transcendentialnumber). And because σ ∈ G(X), there exists fσ : X → Xσ. Equationspi(x) = 0 pσ
i (x) = 0 coefficients rational in ξ coefficients rational inη. Now try to insert in fσ instead of η some algebraic α ∈ Q, and it can beshown that fσ is still an isomorphism for infinitely many α ∈ Q. This givesthe claim.
Theorem 13.5 (Weil) Let X be defined over a finite extension L of M :=M(X). Then X can be defined over M itself if and only if ∀σ ∈ Gal M/Mthere is an isomorphism fσ : X → Xσ such that ∀σ, τ ∈ Gal M/M we have
fστ = f τσ fτ .
47

Analoguous statement holds for M(D) and the field of definition for Xand β, with diagram
X
β !!CCCCCCCCCfσ // Xσ
βσzzzzzzzzz
P1(C)
commuting.Consequence: If Aut X = id, then X is defined over M(X). ⇐ fσ is
unique (generic case for g > 2).
Theorem 13.6 (Coombes/Harbater, Dèbes/Emsalem, J.W., B. Köck)Quasiplatonic curve X can be defined /M(X).
Idea: The canonical projection X → Aut X\X ∼= P1(C) is a Belyi func-tion, assume that the critical points are 0, 1,∞. Let D be the corresponding(regular) dessin on X, M(D) ⊂ Q. Prove first that X, β are defined /M(D).Let r 6= 0, 1, r ∈ M(D) ⊂ C ⊂ C, fix one x ∈ β−1(r), σ ∈ Gal Q/M(D) tomake the following diagram
x& ,,
n
................ X
β
///////////////
// Xσ
βσ
σ(x)
r C
commute. σ(r) = r ⇒ σ(x) ∈ (βσ)−1(r), choose fσ so that fσ(x) = σ(x)⇒ unique choice for fσ and it has been shown that Weil’s conditions aresatisfied! The proof that X can be defined even over M(X) ⊆ M(D) needssome additional arguments.
Exercise 13.1 Show that the elliptic curve can be defined over Q(j(τ)) ⊆Q(g2(τ), g3(τ)).
Exercise 13.2 Suppose X defined /Q, g(X) > 1. (Aut X finite ⇒) Showthat all automorphisms f : X → X are also defined /Q.
48

Lecture 11by Prof. Gareth Jones
14 Regular Embeddings of Complete BipartiteGraphs
14.1 Regular Maps
Every bipartite map B is a quotient of a regular bipartite map B by someA ≤ Aut B. Similarly for maps M. Hence the importance of regular maps.One can try to classify these by type, group, genus or graph.
a) Classifying by type: Study finite quotients of the triangle group ∆ =∆(l,m, n) of a given type (see previous lectures for some ideas). If1l+ 1
m+ 1
n≤ 1 (so ∆ is infinite) then a theorem by Mal’cev states that
a finitely-generated linear group is residually finite (⋂K E ∆ | |∆ :
K| <∞ = 1), so ∆ has infinitely many K E∆ of finite index, so weget infinitely many regular maps of type (l,m, n).
Example 14.1 Taking ∆ = ∆(3, 2, 7) we get infinitely many Hurwitz groupsand Hurwitz surfaces. E.g. Macbeath (1964): PSL2(Fq) is a Hurwitz group⇔ q = 7, or q = p ≡ ±1 mod 7 (p prime), or q = p3, prime p ≡ ±2,±3mod 7. Conder (∼ 1980): An is a Hurwitz group for all n ≥ 168 (and somen < 168).
b) Classifying by group: Difficulty: G usually has many generating pairsx, y. J.D. Dixon (∼ 1964): If x, y are randomly-chosen elements ofG = Sn, then they generate either Sn or An with probabilities → 3
4
(not both elements even) or 14
(both elements even) as n→∞. Thereare similar results for other classes of groups.
c) Classifying by genus: If g = 0 or 1 there are infinitely many regularmaps, but they are well-known (e.g. see Chapter 8 of Coxeter andMoser for g = 1). If g > 1, Hurwitz’s bound |G| ≤ 84(g − 1) impliesthat there are only finitely many regular maps of genus g, and thesecan by classified by hand (for small g) or computer (for larger g).
d) Classifying by graph: Problem: Given a graph G (or class of graphs G),find all regular maps with G as the embedded graph. Equivalently, lookfor G ≤ AutG, transitive on the vertex-set V , with vertex-stabiliser
49

Gv (v ∈ V ) cyclic and transitive on the neighbours of v (induced byrotating the surface around v). Such an embedding can exist only ifG is arc-transitive, i.e. AutG acts transitively on the arcs (=directededges) of G.
Example 14.2 Take G = Kn = ”complete graph on n vertices”. The graphs
•K1 •K2• • •
•
@@@@@@@ K3
~~~~~~~
•
//////////////
•
@@@@@@@
~~~~~~~
•K4
•
are regular embeddings, g = 0.
•
• • •
• • •
•
K5 →”torus”, g = 1. For K6 there’s no embedding and for K7 two exampleson torus (see if you can find them, imitating K5).
Theorem 14.1 (Biggs, 1971) K1 has a regular embedding ⇔ n = pe forsome prime p.
Theorem 14.2 (James & J. 1985) Regular embeddings of Kn classifiedand enumerated.
50

Biggs’s examples are the onlny ones. His construction: Take V = Fn,finite field of order n = pe, unique up to isomorphism. Multiplicative groupF∗n = Fn\0 is cyclic, so choose a generator α. The cyclic order of neighboursof each vertrex v is v + 1, v + α, v + α2, . . ., v + αn−2. Check that this givesa regular embeddingM(α),
G = AutM(α) ∼= AGL1(Fn) = t 7→ at + b | a, b ∈ Fn, a 6= 0 .
M(α) ∼=M(α′)⇔ α, α′ are conjugate under Gal(Fn) ∼= Ce,
where Ce is generated by the Frobenius automorphism t 7→ tp. Therefore
#mapsM(α) =φ(n− 1)
e,
where φ(n− 1) is the number of choices of α generating F∗n ∼= Cn−1 and e isthe size of orbits of Gal(Fn).
Hint for K7: Dessin represents the Fano plane P2(F2). Black/white ver-tices = 7 points & 7 lines. Can you get a regular embedding of K4 from this?Can you get two of them?
14.2 Complete Bipartite Graphs
Take G = Kn,n =”complete bipartite graph with n black vertices and n whitevertices, every black and white pair joined by one edge”, so |V | = 2n and|E| = n2.
We look for embeddings M of Kn,n which are regular as maps, not justas bipartite maps, i.e. AutM (ignoring the vertx-colours) should act tran-sitively on directed edges, not just on edges, so AutM = AutB o C2 whereAutB = G is the automorphism group of the dessin (preserving vertex-colours), and C2 reverses them.
Example 14.3 The Fermat curve xn+yn = 1, with Belyi function β(x, y) =
xn, gives a regular embedding of Kn,n of genus g = (n−1)(n−2)2
, with G =Cn×Cn acting by sending (x, y) to (xζj
n, yζkn); here the automorphism (x, y) 7→
(y, x) transposes black and white vertices, giving AutM = (Cn × Cn) o C2
(isomorphic to wreath product of Cn and C2, Cn o C2). This is the standardembedding Sn of Kn,n.
Thus if ν(n) := ”number of regular embeddings of Kn,n (up to isomor-phism). Then ν(n) ≥ 1 for all n, since Sn exists for all n.
Theorem 14.3 (Nedelar, Škoviera & J. ∼ 2001) ν(n) = 1 (i.e. Sn isthe only regular embedding of Kn,n) ⇔ (n, φ(n)) = 1 ⇔ n = p1 . . . pk, pi
distinct primes, pi - pj − 1 when i 6= j.
51

(Compare with a result of Burnside, ∼ 1900: these are the n for whichthere is only one group of order n, namely Cn. The proofs are independent.)
The asymptotic density of these integers n is (by Erdős, 1948)
number of such integers n ≤ N
N∼ e−γ
log log log Nas N →∞
where γ is Euler’s constant.
Theorem 14.4 (Nedela, Škoviera & J.) If n = pe, prime p > 2, thenν(n) = pe−1.
These maps all have genus g = (n−1)(n−2)2
. They have valency n, and thefaces are all 2n-gons. The groups G = AutB (preserving the vertex-colours)have the form
G = Gf = 〈 g, h | gn = hn = 1, g−1hg = h1+pf 〉,
where f = 1, 2, . . . , e. (If f = e then pf = pe = n, so h1+pf= h, so
G = Cn × Cn withM = Sn)For a given G = Gf , the mapsM correspond to orbits of Aut G on pairs
of elements x, y such that
1. G = XY with X ∩ Y = 1, X = 〈x〉 and Y = 〈y〉, both of order n;
2. some α ∈ Aut G transposes x and y.
(Here x and y represent rotations around a black and a white vertex, αis conjugation of G by an automorphism of M reversing the edge betweenthem.) As representatives of the orbits of Aut G on such pairs, one cantake x = gu, y = guh (or (gh)u, more convinient for Galois theory) whereu = 1, 2, . . . , pe−f and (u, p) = 1.
For each f we have φ(pe−f ) possible choices of u, so summing over f =1, . . . , e we get
∑ef=1 φ(pe−f ) = pe−1 maps M. These correspond to normal
subgroups KE∆(n, n, n), which are also normal in ∆(n, 2, 2n) which contans∆(n, n, n) with index 2.
K E∆(n, n, n) ≤ ∆(n, 2, 2n)
The proof depends on:
Theorem 14.5 (Huppert, 1951) If G is a p-group (|G| is a power of p)for a prime p > 2, and G = XY for cyclic subgroup X and Y , then G ismetacyclic (i.e. there is a cyclic N EG with G/N cyclic).
52

In our case |G| = n2 = p2e, and we can take N = 〈h〉. There areexceptions to Huppert’s Theorem when p = 2, and there are also exceptionalregular embeddings for n = 2e. E.g. n = q = 22:
•
• •
• • •
• •
•
These is an embedding N4 of K4,4 of genus g = 1 6= (n−1)(n−2)2
.
Theorem 14.6 (Du, Kwak, Nedela, Škoviera & J. ∼ 2005) The regu-lar embeddings of Kn,n for n = 2e are:
• these corresponding to Gf for f = 2, 3, . . . , e (not f = 1).
• N4 if e = 2.
• four similar exceptions for each e ≥ 3.
Recent result (Apice 2006): complete classification for all n.What about the associated algebraic curves, Galois orbits, fields of defi-
nition, etc. Jürgen, Manfred Streit, Antoine Coste.
53

Lecture 12by Prof. Jürgen Wolfart
15 Generalised Fermat CurvesTheorem 15.1 Let X be a quasiplatonic curve with a regular dessin D oftype (l,m, n), and suppose that for any dessin D′ of the same type Aut D′ ∼=Aut D implies D ∼= D′. Then X can be defined over Q.
Proof. l,m, n is invariant under the action of GC or Gal Q/Q, and moreover
Aut Xσ ∼= Aut X.
⇒ Aut Dσ ∼= Aut D. From the hypothesis therefore follows Dσ ∼= D. ⇒G(D) = GC ⇒ M(D) = Q ⇒ X can be defined over Q.
Theorem 15.1 applies to all quasiplatonic curves up to g = 5.Recall: Fermat curves Fn, n > 3, have a regular dessin of type (n, n, n),
based on Kn,n. Suppose now that n = pe > 3 (odd prime power) and supposethat all dessins are based on Kn,n, and they are regular as maps (i.e. thereis edge-transitive automorphism group and moreover a colour-exchanging(orientable) involution oo // • . Recall that then [G.J., Nedela, Škoviera]
Aut D ∼= Cn o Cn := 〈 g, h | gn = hn = 1, hg := g−1hg = h1+pf 〉 = Gf
(colour-preserving subgroup) for some f = 1, . . . , e
• the Gf are pairwise non-isomorphic
• ∀ f = 1, . . . , e there are quotients ∆/Kf,u∼= Gf for ∆ = 〈n, n, n〉 by
the kernel Kf,u of the homomorphism γ0 7→ gu, γ1 7→ (gh)u for some ucoprime to p
• these kernels Kf,u, Kf,v are different⇔ u 6≡ v mod pn−f (giving pe−f−pe−f−1 different surface groups if f < e)
• the case f = e we have Ge∼= Cn × Cu ⇒ Ke,1 = [∆, ∆] and Ke,1\H ∼=
Fn.
Call Xf,u := Kf,u\H for f = 1, . . . , e and u ∈ (Z/pe−fZ)∗ ”generalised Fermatcurves”.
54

Theorem 15.2 (G.J.,Manfred Streit, J.W.) For fixed n = pe odd andf ∈ 1, . . . e , these Xf,u form one Galois orbit. Their moduli field M(Xf,u)(= a minimal field of definition) is
Q(η), η = exp
(2πi
pe−f
).
Ideas for the proof:
1. Show that Xf,u∼= Xg,v ⇔ f = g and u ≡ v mod pe−f . Gf
∼= Gg ⇔f = g. Therefore the first implication is done. Xf,u
∼= Xf,v ⇔ Kf,u andKf,v conjugate in PSL2 R (even in 〈2, 3, 2n〉). That possibility can beexcluded.
2. For all σ ∈ Gal Q/Q consider Xσf,u.
Ramifications are preservedRegularity is preserved
Aut Xf,u is preserved
⇒ Xσf,u∼= some Xf,v, v ∈ (Z/pe−fZ)∗.
⇒ Galois orbits are parts of Xf,u |u ∈ (Z/pe−fZ)∗
3. Acting on Xf,u (and the dessin), g has pf (white) fixed points and ghhas pf (black) fixed points. Gf is considered as automorphism group∼= ∆/Kf,u, for the
• •
•kkkkkkkkkk •
SSSSSSSSSS γ0
KK
fixed point of γ0
OO
γ0 7→ gu ⇒ g = (gu)u′
(where uu′ ≡ 1 mod n) number of the fixed points calculate the index
(NGf(〈g〉) : 〈g〉) = pf = (NGf
(〈hg〉) : 〈hg〉)
4. Locally in the fixed points, γ0 and γ1 behave like z 7→ ζnz+ ”higher z-powers”. Fixed point ↔ 0 = z. ⇒ gu has also multiplier ζ = ζn in thecorresponding fixed point ⇒ g has multiplier ζu′ in the correspondingfixed point. All g-fixed points form an orbit under
⟨hpe−f
⟩-orbit and
g has the same multiplier ζu′ in all its fixed points! Also gh has themultiplier ζu′ (u′u ≡ 1 mod n) in all its • fixed points. ⇒ In its family,Xf,u is characterised by the multipliers ζu′ of g and gh in their fixedpoints. Fixed points of g: action locally by z 7→ ζu′z+ ”higher terms”.
55

5. Behaviour of the multipliers under σ ∈ Gal Q/Q. Suppose g ∈ Aut Xwith fixed points P ∈ X and multiplier ξ⇒ on Xσ, g has fixed point P σ
with multiplier σ(ξ). Choose for the local chart some X → C globallymeromorphic, defined over Q, P 7→ 0 simple zero in P , multipliers arealways roots of unity (⇐ finite order), ξ 7→ σ(ξ) root of unity, sameorder.
6. σ ∈ Gal Q/Q, σ|Q(η) = idQ(η), where η = e2πi
pe−f . σ(ζu′) = ζv′ (primitiventh-root of unity) with v′ ≡ u′ mod pe−f ⇔ v ≡ u mod pe−f ⇔Xf,u
∼=Xf,v ⇒ σ ∈ G(Xf,u) ⇒ Q(η) is a field of definition. Gal Q/Q actstransitively on the primitive nth roots of unity ⇒ acts transitively onXf,u ⇒ they form a Galois orbit. M(Xf,u) = Q(η) is a field ofdefinition.
Theorem 15.3 Let n = pe > 3 be an odd prime power and f ≥ e2. Then we
have a (singular, affine) model for Xf,1, given by the equations
vn = β(β − 1)
wpe−f
= 1− β
zpf
= w−r
pe−f−1∏k=0
(w − ηk)ak
where a := p2f−e, r :=((1 + pf )pe−f − 1
)/pe (∈ N, coprime to p).
Idea: Covering groups ↔ Galois groups of extensions of function fields.
G ∈ σ Y
f //
!!CCCCCCCCCC C
X (f σ) (σ−1f) mero on Y .
Kf,u// 1
Γ〈h〉 // 〈h〉C
quotient Cn %%KKKKKKKKKK
∆ // // Gf = 〈g, h〉
56

Xf,u
wwwwwwwwwwwww
C(β, v) withvn = rationalfunction of β
Cu-extensionof C(β)
##GGGGGGGGGGGΓ〈h〉\H
FFFFFFFFFFFF
C(β) C ∼= ∆\H
Equations for Xf,u = Kf,u\H ⇐ algebraic relations in the correspondingfunction field. This is the composite field of the function field for Γ〈h〉\Hand Γ〈g〉\H where Γ〈h〉 and Γ〈g〉 are the preimages of 〈h〉 and 〈g〉 under theepimorphism ∆→ Gf . Since
Γ〈h〉\H→ ∆\H = C
is a cyclic covering ramified with multiplicity n above 0, 1,∞, with an ad-ditional symmetry between 0 and 1, we get C(β, v) as function field for thecovering space with vn = β(β−1). The corresponding construction for Γ〈g〉\His more complicated, since it needs a two-step tower of normal coverings.
57

Exercises
16 Some Hints Concerning ExercisesExercise 1.1
Fn projective Fermat curve of exponent n, then Aut Fn ⊆ (Cn×Cn) o S3
(semidirect product), see Gareth’s Lecture 8. Moreover ”=” holds if n > 3because its surface group K is the commutator subgroup [∆, ∆] of the trianglegroup ∆ = 〈n, n, n〉, and Aut Fn = N(K)/K, N(K) = 〈2, 3, 2n〉 containing∆ as a normal subgroup with quotient S3. In fact, the hyperbolic trianglefor the construction of 〈2, 3, 2n〉 results from that for 〈n, n, n〉 by barycentricsubdivision, and it can be shown that 〈2, 3, 2n〉 is maximal Fuchsian group,so N(K) cannot be larger than 〈2, 3, 2n〉 (the analogous statement for n = 3,i.e. for 〈2, 3, 6〉 would be definitely wrong!).
Exercise 1.2/4.2The genus of the (compact) hyperelliptic curve with affine equation y2 =
q(x), deg q =
2g + 1
2g + 2
with
2
1
points above x = ∞ is g by appli-
cation of Riemann-Hurwitz to the mapping f : (x, y) 7→ x of degree 2: It isramified in 2g + 2 points with multiplicity 2, hence we have in fact
2g − 2 = 2 · (−2) +∑
(multp f − 1) = −4 + (2g + 2) · 1.
In the special case q(x) = xn − 1 =∏n
k=1(x− ζkn)⇒
X → C→ C(x, y) 7→ x 7→ xn
ramified above
0 in 2 points, mult = n
1 in n points, mult = 2
∞ in 1 point, mult = 2n for 2|n∞ in 2 points, mult = n for 2 - n
defines a Belyi function of deg 2n and the dessin for this Belyi function lookslike two planes with this bipartite graph,
• •
~~~~~~~
@@@@@@@ •
~~~~~~~
@@@@@@@ •
• •
glued in the black points (and the point ∞ if n is even).
58

A picture in H ∼= D can be given and by a 2n-sided polygon
•
•
in the case 2|n and a 2(n− 1)-sided polygon, subdivided in two cells
••
•
========
========
•
•
if 2 - n.Exercise 4.3A Belyi function for y2 = x(x− 1)(x− ζ3
3√2is formally the same (x, y) 7→
4x3(1− x3) as if ζ3 is replaced by 1, but with different ramifications, so thedessin now looks like
~~~~~~~ @@ • •
• @@
• @@
@@
@@ •(
ζ33√2
,0)
vvvvvvvvv• @@
(0,0) ( 3√2,y3)
•(1,0) •
( 3√2,−y3) (0,0)
in a fundamental parallellogram for the elliptic curve. For ζ23 = ζ3 instead of
ζ3 a mirror image of this dessin arises.
59

Exercise 7.1β 7→ 1− β exchanges the colours of the bipartite graph, β 7→ 1
βpreserves
β = 1 and exchanges zeros and poles, hence cell centers and 0-vertices⇒ thepole orders of β are the zero orders of that modified dessin = 1
2#”border
edges of the cell”, but the ”inner edges” having the face on both sides haveto be counted twice!
OOOOOOO
ooooooo
• • •
???
OOOOOOO
ooooooo
•
β 7→ 16β(β − 3
4)2
replaces 0 1
• by 0 1
4
•34
1• . (Idea: Take 1
2(1+Tn(2β−1)),
n odd, to insert more vertices with Tn the nth Tshebychev polynomial)
60
![¥IIÌ 01 S o U H S 9 0 à S Il s D b 111 Il S 01 111 H U 00 ...s o S 94 o S s Il 94 41 Ill H à Ill rH ùl s s ¥IIÌ 10 ¥]ÌII rn S 94 Il S s à S 9-4- > o . r 1 01 111 u Il 94](https://static.fdocuments.pl/doc/165x107/5ecd2d7d404b97379a3679a6/iioe-01-s-o-u-h-s-9-0-f-s-il-s-d-b-111-il-s-01-111-h-u-00-s-o-s-94-o-s-s.jpg)



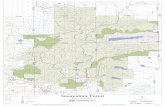




![· DOMO [latin] domus, domu : maison, lieu d'accueil, habitation . 3 Wall Page 4 Nuancier Français Page 7 Nuancier International Page 14. 4 Une révolution murale Utiliser les surfaces](https://static.fdocuments.pl/doc/165x107/5c72cd8c09d3f2b92e8c437e/-domo-latin-domus-domu-maison-lieu-daccueil-habitation-3-wall-page.jpg)


![jp.yamaha.com · io a a . St —77 U txt 1.1] s U s s V o a s 94. 6 u s a a S o s s o 00 00 St cff 1 o S s rìt N s S N S a S u o (5 s 08 U rts s 4] Ilk S O s 5 rx S . s q 94 o s](https://static.fdocuments.pl/doc/165x107/5f8c356f9e2284314f5f098d/jp-io-a-a-st-a77-u-txt-11-s-u-s-s-v-o-a-s-94-6-u-s-a-a-s-o-s-s-o-00-00-st.jpg)






